算法总结 DAY_03

寻找重复的数

LeetCode 287. find-the-duplicate-number

题目：

image-20220319145857496

题解

哈希表

不满足空间O(1)的要求

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        // unordered_map<int, int> map;
        // for(int i=0; i<nums.size(); i++){
        //     map[nums[i]] ++;
        //     if(map[nums[i]] > 1){
        //         return nums[i];
        //     }
        // }
        set<int> s;
        for(int i=0; i<nums.size(); i++){
            if(s.count(nums[i]) == 1){
                return nums[i];
            }
            s.insert(nums[i]);
        }
        return 0;
    }
};

二分查找

image-20220320115902117

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size();
        int l = 1, r = n - 1, ans = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            for (int i = 0; i < n; ++i) {
                cnt += nums[i] <= mid;
            }
            if (cnt <= mid) {
                l = mid + 1;
            } else {
                r = mid - 1;
                ans = mid;
            }
        }
        return ans;
    }
};

复杂度分析

  • 时间复杂度：O(nlogn)，其中 n 为 nums 数组的长度。二分查找最多需要二分 O(logn) 次，每次判断的时候需要O(n) 遍历 nums 数组求解小于等于 mid 的数的个数，因此总时间复杂度为 O(nlogn)。
  • 空间复杂度：O(1)。我们只需要常数空间存放若干变量。

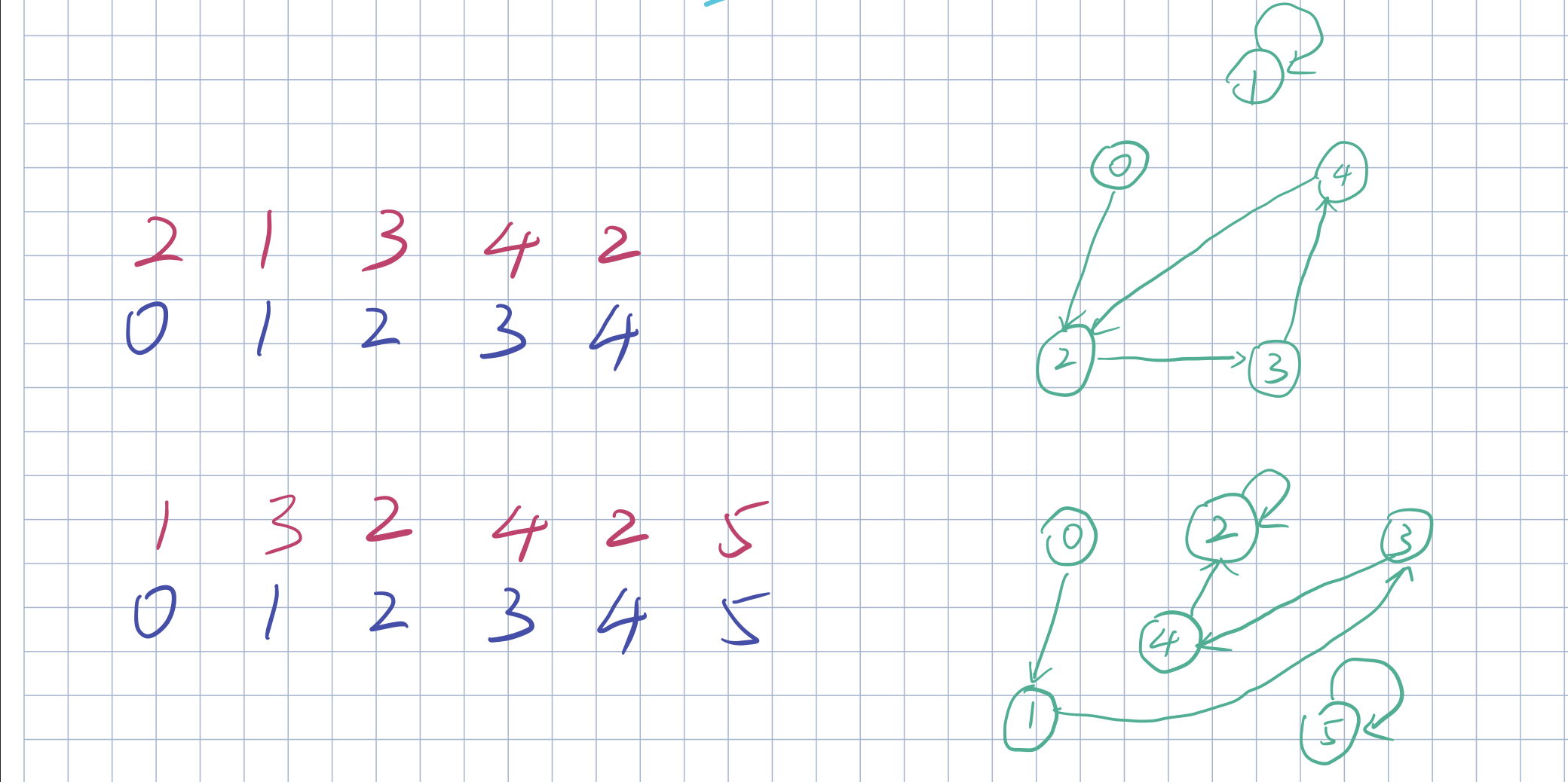
快慢指针

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = 0, fast = 0;
        //知识点1；弗洛伊德判圈算法
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while (slow != fast);
        slow = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
};

复杂度分析

  • 时间复杂度：O(n)。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。
  • 空间复杂度：O(1)。我们只需要常数空间存放若干变量。

知识点拓展

弗洛伊德判圈算法

image-20220321170935876 image-20220320120222194 image-20220321170749874

预测赢家

LeetCode 486. predict-the-winner

题目：

image-20220321164123782

题解

递归到动态规划的过程参考：从暴力递归到动态规划

递归

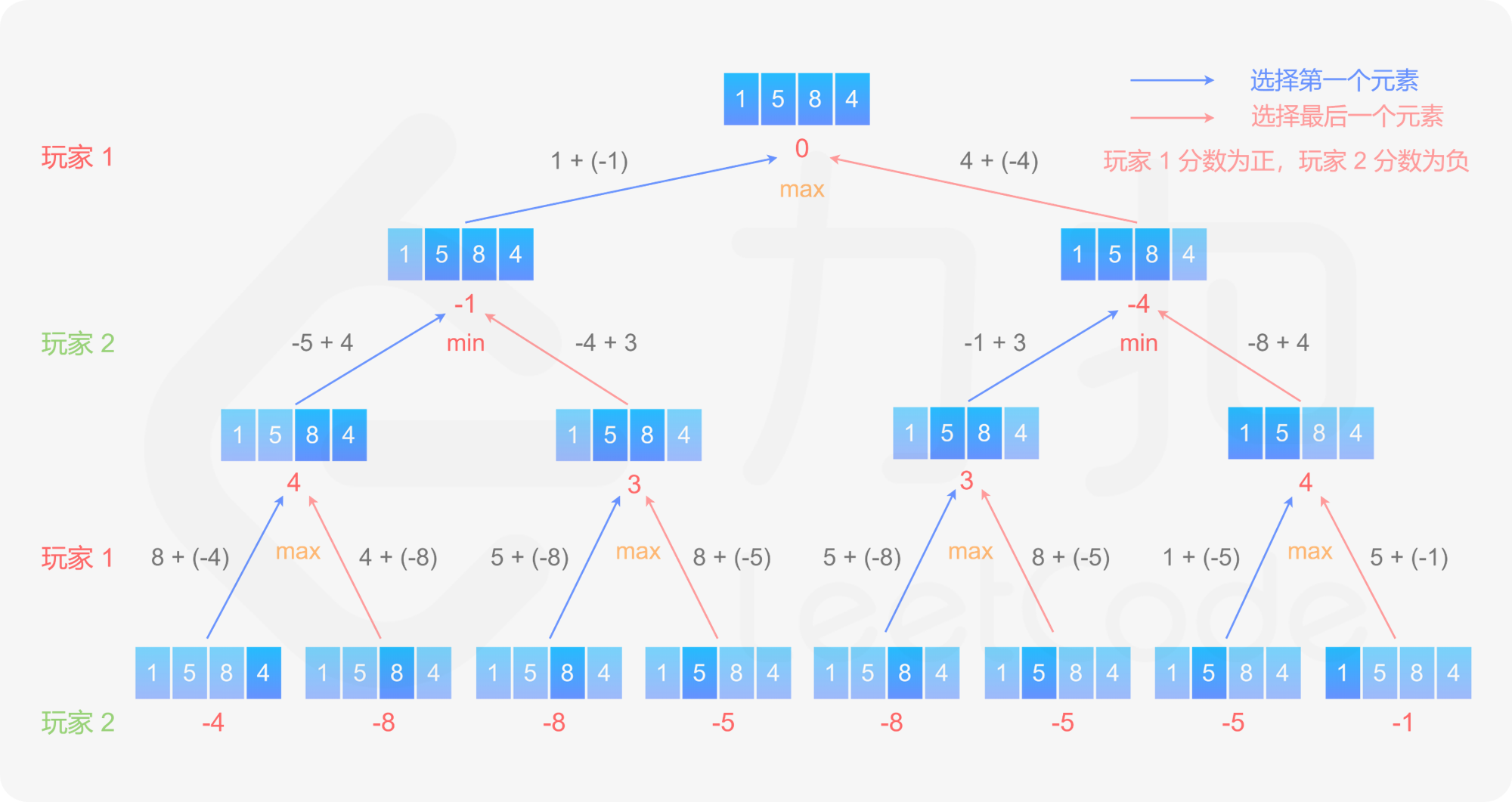
fig1 
class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        return total(nums, 0, nums.size() - 1, 1) >= 0;
    }

    int total(vector<int>& nums, int start, int end, int turn) {
        if (start == end) {
            return nums[start] * turn;
        }
        int scoreStart = nums[start] * turn + total(nums, start + 1, end, -turn);
        int scoreEnd = nums[end] * turn + total(nums, start, end - 1, -turn);
        return max(scoreStart * turn, scoreEnd * turn) * turn;
    }
};

image-20220321165942045

动态规划

dp[i][j]表示当数组剩下的部分为下标 i 到下标 j 时，即在下标范围 [i, j] 中，当前玩家与另一个玩家的分数之差的最大值，注意当前玩家不一定是先手。

最后判断dp[0][n-1] 的值，如果大于或等于 0，则先手得分大于或等于后手得分，因此先手成为赢家，否则后手成为赢家。

image-20220321164231124 
class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        int n = nums.size();
        int dp[n][n];
        for(int i=0; i<n; i++){
            dp[i][i] = nums[i];
        }
        for(int i=n-2; i>=0; i--){
            for(int j=i+1; j<n; j++){
                dp[i][j] = max(dp[i][i]-dp[i+1][j], dp[j][j]-dp[i][j-1]);
            }
        }
        return dp[0][n-1] >= 0;
    }
};

官方题解：

计算 dp 的第 i 行的值时，只需要使用到 dp 的第 i 行和第 i+1 行的值，因此可以使用一维数组代替二维数组，对空间进行优化。

class Solution {
public:
    bool PredictTheWinner(vector<int>& nums) {
        int length = nums.size();
        auto dp = vector<int>(length);
        for (int i = 0; i < length; i++) {
            dp[i] = nums[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[j] = max(nums[i] - dp[j], nums[j] - dp[j - 1]);
            }
        }
        return dp[length - 1] >= 0;
    }
};
image-20220321165005830

前K个高频单词

LeetCode 692. top-k-frequent-words

题目：

image-20220321102926071

题解

哈希表+排序

使用哈希表记录每种单词出现的次数，再进行排序。

使用map与unordered_map的区别：

map底层采用的是红黑树的实现，Key值默认按由小到大排序，符号题目要求，因此重写stable_sort()函数时，无需比较key值；

而unordered_map底层采用哈希表的实现，内部就是无序的，因此重写sort()函数时，需比较key值。

class Solution {
public: 
    vector<string> topKFrequent(vector<string>& words, int k) {
        // unordered_map<string, int> map;
        map<string, int> map;
        vector<string> ans;
        for(auto& w : words){
            map[w] ++;
        }
        vector<pair<string, int>> vecs;
        // for (auto it = map.begin();it!= map.end();it++) {
        //     vecs.push_back(make_pair(it->first, it->second));
        // }
        // 知识点1： assign() 函数的使用
        vecs.assign(map.begin(), map.end());
        // 知识点2： sort() 函数重写
        // 知识点3. stable_sort()与sort()的区别
        stable_sort(vecs.begin(), vecs.end(), [](pair<string, int>a, pair<string, int> b) ->    bool{
        return a.second > b.second;
        });
        for (int i=0; i<k; i++){
            ans.push_back(vecs[i].first);
        }
        return ans;
    }
};

官方题解：

class Solution {
public:
    vector<string> topKFrequent(vector<string>& words, int k) {
        unordered_map<string, int> cnt;
        for (auto& word : words) {
            ++cnt[word];
        }
        vector<string> rec;
        for (auto& [key, value] : cnt) {
            rec.emplace_back(key);
        }
        sort(rec.begin(), rec.end(), [&](const string& a, const string& b) -> bool {
            return cnt[a] == cnt[b] ? a < b : cnt[a] > cnt[b];
        });
        rec.erase(rec.begin() + k, rec.end());
        return rec;
    }
};

image-20220321104004861

优先队列

思路及算法

对于前 k 大或前 k 小这类问题，有一个通用的解法：优先队列。优先队列可以在 O(logn) 的时间内完成插入或删除元素的操作（其中 n 为优先队列的大小），并可以 O(1) 地查询优先队列顶端元素。

在本题中，我们可以创建一个小根优先队列（顾名思义，就是优先队列顶端元素是最小元素的优先队列）。我们将每一个字符串插入到优先队列中，如果优先队列的大小超过了 k，那么我们就将优先队列顶端元素弹出。这样最终优先队列中剩下的 k 个元素就是前 k 个出现次数最多的单词。

（可以通过此方法解决数量级较小的Top-K问题）

class Solution {
public:
    vector<string> topKFrequent(vector<string>& words, int k) {
        unordered_map<string, int> cnt;
        for (auto& word : words) {
            cnt[word]++;
        }
        auto cmp = [](const pair<string, int>& a, const pair<string, int>& b) {
            return a.second == b.second ? a.first < b.first : a.second > b.second;
        };
        priority_queue<pair<string, int>, vector<pair<string, int>>, decltype(cmp)> que(cmp);
        for (auto& it : cnt) {
            que.emplace(it);
            if (que.size() > k) {
                que.pop();
            }
        }
        vector<string> ret(k);
        for (int i = k - 1; i >= 0; i--) {
            ret[i] = que.top().first;
            que.pop();
        }
        return ret;
    }
};

image-20220321110804418

知识点拓展

assign() 函数的使用

STL中不同容器之间是不能直接赋值的，assign（）可以实现不同容器但相容的类型赋值，

list<string> names;
vector<const char*> oldstyle = { "I","love","you" };
//names = oldstyle;错误！不同的类型不能执行"="操作
names.assign(oldstyle.cbegin(), oldstyle.cend());
list<string>::iterator it;
for (auto it = names.begin(); names.begin() != names.end(); it++)
        cout << *it << " ";

img

sort() 函数的重写

sort函数有三种用法：

一：对基本类型数组从小到大排序

sort( 数组名+n1，数组名+n2)；

将数组中下标从n1到n2的元素进行从小到大排序，不包括n2，通过n1,n2 可以对整个或者部分数组排序

二：对元素类型为T的基本类型数组从大到小排序

sort( 数组名+n1，数组名+n2，greater<T>());

T对应各种元素类型

同样，将数组中下标从n1到n2的元素进行从大到小排序，不包括n2，通过n1,n2 可以对整个或者部分数组排序；

三：第三种自定义排序规则

sort(数组名+n1，数组名+n2，排序规则结构名）;

排序规则结构体定义：

struct 结构名{
     bool operator()(const T &a1, const T &a2){
          return    ;
     } 
};

返回值为true说明a1应该排在a2前面，false则相反，T对应元素类型。

或者直接写在sort()函数中：

sort(vecs.begin(), vecs.end(), [](pair<string, int>a, pair<string, int> b) ->    bool{
        return a.second > b.second;
        });

举个例子：

排序规则为按个位数从小到大排序：

struct Rule1{ 
    bool operator()(const int &a1, const int &a2){
    	return (a1%10)<(a2%10);
	} 
};

stable_sort() 与 sort() 函数的区别

stable_sort()可以对vector的某个成员进行排序，而且可保证相等元素的原本相对次序在排序后保持不变。

例如，如果你写一个比较函数:

bool less_len(const string &str1, const string &str2)
{
        return str1.length() < str2.length();
}

此时，**”apples” 和 “winter” 就是相等的，如果在”apples” 出现在”winter”前面，用带stable的函数排序后，他们的次序一定不变，如果你使用的是不带”stable”的函数排序，那么排序完 后，”winter”有可能在”apples”的前面。**

数据流的中位数

LeetCode 295. find-median-from-data-stream

题目：

image-20220321114211354

题解

优先队列

image-20220321114514930

class MedianFinder {
public:
    // 知识点1： 优先队列
    priority_queue<int, vector<int>, less<int>> queMin;
    priority_queue<int, vector<int>, greater<int>> queMax;

    MedianFinder() {}

    void addNum(int num) {
        if (queMin.empty() || num <= queMin.top()) {
            queMin.push(num);
            if (queMax.size() + 1 < queMin.size()) {
                queMax.push(queMin.top());
                queMin.pop();
            }
        } else {
            queMax.push(num);
            if (queMax.size() > queMin.size()) {
                queMin.push(queMax.top());
                queMax.pop();
            }
        }
    }

    double findMedian() {
        if (queMin.size() > queMax.size()) {
            return queMin.top();
        }
        return (queMin.top() + queMax.top()) / 2.0;
    }
};

复杂度分析

  • 时间复杂度：addNum: O(logn)，其中 n 为累计添加的数的数量。

    ​ findMedian: O(1)。

  • 空间复杂度：O(n)，主要为优先队列的开销。

有序集合+双指针

image-20220321142308045

class MedianFinder {
    multiset<int> nums;
    multiset<int>::iterator left, right;

public:
    MedianFinder() : left(nums.end()), right(nums.end()) {}

    void addNum(int num) {
        const size_t n = nums.size();

        nums.insert(num);
        if (!n) {
            left = right = nums.begin();
        } else if (n & 1) {
            if (num < *left) {
                left--;
            } else {
                right++;
            }
        } else {
            if (num > *left && num < *right) {
                left++;
                right--;
            } else if (num >= *right) {
                left++;
            } else {
                right--;
                left = right;
            }
        }
    }

    double findMedian() {
        return (*left + *right) / 2.0;
    }
};

复杂度分析

  • 时间复杂度：addNum: O(logn)，其中 n 为累计添加的数的数量。

    ​ findMedian: O(1)。

  • 空间复杂度：O(n)，主要为有序集合的开销。

知识点拓展

优先队列

包含头文件#include <queue>, 他和queue不同的就在于我们可以自定义其中数据的优先级, 让优先级高的排在队列前面,优先出队

优先队列具有队列的所有特性，包括基本操作，只是在这基础上添加了内部的一个排序，它本质是一个堆实现的和队列基本操作相同:

top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾 (并排序)
emplace 原地构造一个元素并插入队列
pop 弹出队头元素
swap 交换内容

定义：priority_queue<Type, Container, Functional>

Type 就是数据类型，Container 就是容器类型（Container必须是用数组实现的容器，比如vector,deque等等，但不能用 list。STL里面默认用的是vector），Functional 就是比较的方式，当需要用自定义的数据类型时才需要传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大顶堆。

//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;

//greater和less是std实现的两个仿函数（就是使一个类的使用看上去像一个函数。其实现就是类中实现一个operator()，这个类就有类似函数的行为，就是一个仿函数类了）

基本类型例子：

#include<iostream>
#include <queue>
using namespace std;
int main() {
    //对于基础类型 默认是大顶堆
    priority_queue<int> a; 
    //等同于 priority_queue<int, vector<int>, less<int> > a;
    priority_queue<int, vector<int>, greater<int> > c;  //这样就是小顶堆
    priority_queue<string> b;
    
    for (int i = 0; i < 5; i++) {
        a.push(i);
        c.push(i);
    }
    while (!a.empty()) {
        cout << a.top() << ' ';
        a.pop();
    } 
    cout << endl;
    
    while (!c.empty()) {
        cout << c.top() << ' ';
        c.pop();
    }
    cout << endl;
    
    b.push("abc");
    b.push("abcd");
    b.push("cbd");
    while (!b.empty()) {
        cout << b.top() << ' ';
        b.pop();
    } 
    cout << endl;
    return 0;
}

输出

4 3 2 1 0
0 1 2 3 4
cbd abcd abc

pari的比较，先比较第一个元素，第一个相等比较第二个

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main() {
    priority_queue<pair<int, int> > a;
    pair<int, int> b(1, 2);
    pair<int, int> c(1, 3);
    pair<int, int> d(2, 5);
    a.push(d);
    a.push(c);
    a.push(b);
    while (!a.empty()) {
        cout << a.top().first << ' ' << a.top().second << '\n';
        a.pop();
    }
}

输出

2 5
1 3
1 2

对于自定义类型

#include <iostream>
#include <queue>
using namespace std;

//方法1
struct tmp1 //运算符重载<
{
    int x;
    tmp1(int a) {x = a;}
    bool operator<(const tmp1& a) const{
        return x < a.x; //大顶堆
    }
};
//方法2
struct tmp2 //重写仿函数
{
    bool operator() (tmp1 a, tmp1 b) {
        return a.x < b.x; //大顶堆
    }
};
int main() 
{
    tmp1 a(1);
    tmp1 b(2);
    tmp1 c(3);
    priority_queue<tmp1> d;
    d.push(b);
    d.push(c);
    d.push(a);
    while (!d.empty()) {
        cout << d.top().x << '\n';
        d.pop();
    }
    cout << endl;
    priority_queue<tmp1, vector<tmp1>, tmp2> f;
    f.push(c);
    f.push(b);
    f.push(a);
    while (!f.empty()) {
        cout << f.top().x << '\n';
        f.pop();
    }
}

输出

3
2
1

3
2
1

参考链接：(44条消息) c++优先队列(priority_queue)用法详解_吕白_的博客-CSDN博客_c++ 优先队列

寻找重复的子树

LeetCode 652. find-duplicate-subtrees

题目：

image-20220321145143286

题解

序列化+DFS+哈希表

思路

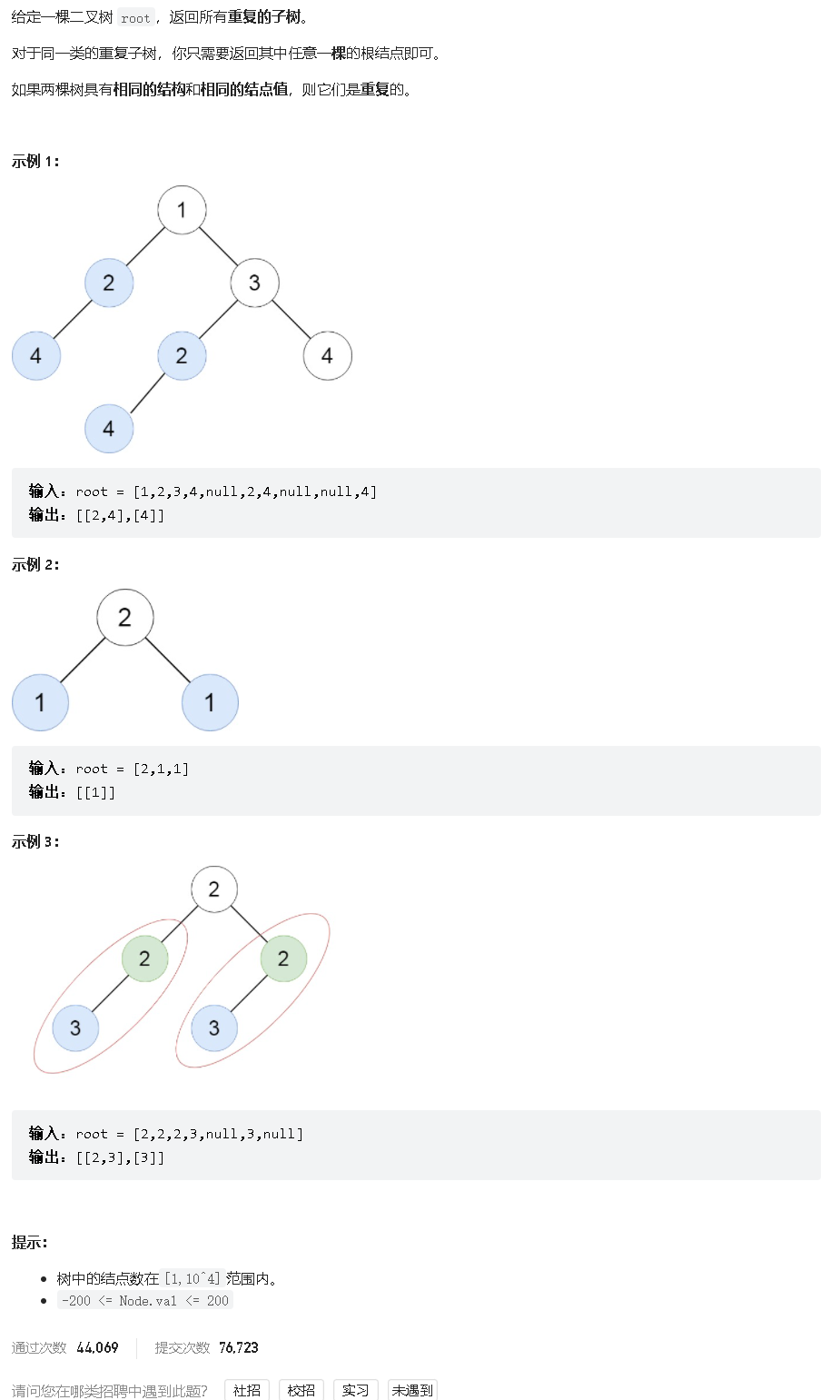
序列化二叉树（先序）：

  1
 / \
2   3
   / \
  4   5

例如上面这棵树序列化结果为 1,2,#,#,3,4,#,#,5,#,#。每棵不同子树的序列化结果都是唯一的。

算法

使用深度优先搜索，其中递归函数返回当前子树的序列化结果。把每个节点开始的子树序列化结果保存在 map 中，然后判断是否存在重复的子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string dfs(TreeNode* root){
        if(root == nullptr){
            return "#";
        }
        string n = to_string(root->val)+','+dfs(root->left)+','+dfs(root->right);
        map[n] ++;
        if(map[n] == 2){
            ans.push_back(root);
        } 
        return n;
    }
    vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
        dfs(root);
        return ans;
    }
private:
    unordered_map<string, int> map;
    vector<TreeNode*> ans;
};

复杂度分析

  • 时间复杂度：O(N^2)，其中 NN 是二叉树上节点的数量。遍历所有节点，在每个节点处序列化需要时间 O(N)。
  • 空间复杂度：O(N^2)，count 的大小。

唯一标识符

image-20220321155821996

class Solution {
    int t;
    Map<String, Integer> trees;
    Map<Integer, Integer> count;
    List<TreeNode> ans;

    public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
        t = 1;
        trees = new HashMap();
        count = new HashMap();
        ans = new ArrayList();
        lookup(root);
        return ans;
    }

    public int lookup(TreeNode node) {
        if (node == null) return 0;
        String serial = node.val + "," + lookup(node.left) + "," + lookup(node.right);
        int uid = trees.computeIfAbsent(serial, x-> t++);
        count.put(uid, count.getOrDefault(uid, 0) + 1);
        if (count.get(uid) == 2)
            ans.add(node);
        return uid;
    }
}

复杂度分析

  • 时间复杂度：O(N)，其中 NN 二叉树上节点的数量，每个节点都需要访问一次。
  • 空间复杂度：O(N)，每棵子树的存储空间都为 O(1)。