算法总结 DAY_02

省份数量

LeetCode 547. number-of-provinces

题目：

image-20220314162659080 image-20220314162814544

题解

深度优先搜索

深度优先搜索的思路是很直观的。遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过矩阵 isConnected 得到与该城市直接相连的城市有哪些，这些城市和该城市属于同一个连通分量，然后对这些城市继续深度优先搜索，直到同一个连通分量的所有城市都被访问到，即可得到一个省份。遍历完全部城市以后，即可得到连通分量的总数，即省份的总数。

class Solution {
public:
    void dfs(vector<vector<int>>& isConnected, vector<int>& visited, int city, int i){
        for(int j=0; j<city; j++){  
            if(visited[j] != 1 && isConnected[i][j] == 1){
                visited[j] = 1;
                dfs(isConnected, visited, city, j);
            }
        }
    }
    int findCircleNum(vector<vector<int>>& isConnected) {
        int provience = 0;
        int city = isConnected.size();
        vector<int> visited(city);
        for(int i=0; i<city; i++){    
            if(visited[i] != 1){
               dfs(isConnected, visited, city, i);
                provience++; 
            }
        }
        return provience;
    }
};

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是城市的数量。需要遍历矩阵 n 中的每个元素。

  • 空间复杂度：O(n)，其中 n 是城市的数量。需要使用数组 visited 记录每个城市是否被访问过，数组长度是 n，递归调用栈的深度不会超过 n。

广度优先搜索

也可以通过广度优先搜索的方法得到省份的总数。对于每个城市，如果该城市尚未被访问过，则从该城市开始广度优先搜索，直到同一个连通分量中的所有城市都被访问到，即可得到一个省份。

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int provinces = isConnected.size();
        vector<int> visited(provinces);
        int circles = 0;
        queue<int> Q;
        for (int i = 0; i < provinces; i++) {
            if (!visited[i]) {
                Q.push(i);
                while (!Q.empty()) {
                    int j = Q.front(); Q.pop();
                    visited[j] = 1;
                    for (int k = 0; k < provinces; k++) {
                        if (isConnected[j][k] == 1 && !visited[k]) {
                            Q.push(k);
                        }
                    }
                }
                circles++;
            }
        }
        return circles;
    }
};

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是城市的数量。需要遍历矩阵 isConnected 中的每个元素。

  • 空间复杂度：O(n)，其中 n 是城市的数量。需要使用数组 visited 记录每个城市是否被访问过，数组长度是 n，广度优先搜索使用的队列的元素个数不会超过 n。

并查表

计算连通分量数的另一个方法是使用并查集。初始时，每个城市都属于不同的连通分量。遍历矩阵 isConnected，如果两个城市之间有相连关系，则它们属于同一个连通分量，对它们进行合并。

遍历矩阵 isConnected 的全部元素之后，计算连通分量的总数，即为省份的总数。

class Solution {
public:
    int Find(vector<int>& parent, int index) {
        if (parent[index] != index) {
            parent[index] = Find(parent, parent[index]);
        }
        return parent[index];
    }

    void Union(vector<int>& parent, int index1, int index2) {
        parent[Find(parent, index1)] = Find(parent, index2);
    }

    int findCircleNum(vector<vector<int>>& isConnected) {
        int provinces = isConnected.size();
        vector<int> parent(provinces);
        for (int i = 0; i < provinces; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < provinces; i++) {
            for (int j = i + 1; j < provinces; j++) {
                if (isConnected[i][j] == 1) {
                    Union(parent, i, j);
                }
            }
        }
        int circles = 0;
        for (int i = 0; i < provinces; i++) {
            if (parent[i] == i) {
                circles++;
            }
        }
        return circles;
    }
};

image-20220314164525963

知识点拓展

并查集的概念与性质

初始化

int fa[MAXN];
inline void init(int n)
{
    for (int i = 1; i <= n; ++i)
        fa[i] = i;
}

假如有编号为1, 2, 3, …, n的n个元素，我们用一个数组fa[]来存储每个元素的父节点（因为每个元素有且只有一个父节点，所以这是可行的）。一开始，我们先将它们的父节点设为自己。

合并

int find(int x)
{
    if(x == fa[x])
        return x;
    else{
        fa[x] = find(fa[x]);  //父节点设为根节点
        return fa[x];         //返回父节点
    }
}

只要我们在查询的过程中，把沿途的每个节点的父节点都设为根节点即可。

查询

int find(int x)
{
    if(fa[x] == x)
        return x;
    else
        return find(fa[x]);
}

我们用递归的写法实现对代表元素的查询：一层一层访问父节点，直至根节点（根节点的标志就是父节点是本身）。要判断两个元素是否属于同一个集合，只需要看它们的根节点是否相同即可。

参考链接：算法学习笔记(1) : 并查集 - 知乎 (zhihu.com)

第一个只出现一次的字符

面试题50. 第一个只出现一次的字符

题目：

image-20220317171031229

题解

哈希表

我们可以对字符串进行两次遍历。

在第一次遍历时，我们使用哈希映射统计出字符串中每个字符出现的次数。在第二次遍历时，我们只要遍历到了一个只出现一次的字符，那么就返回该字符，否则在遍历结束后返回空格。

class Solution {
public:
    char firstUniqChar(string s) {
        unordered_map<char, int> map;
        for(int i=0; i<s.size(); i++){
            map[s[i]] ++;
        }
        for(int i=0; i<s.size(); i++){
            if(map[s[i]]==1)
                return s[i];
        }
        return ' ';
    }
};

复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 s 的长度。我们需要进行两次遍历。
  • 空间复杂度：O(∣Σ∣)，其中 Σ 是字符集，在本题中 s 只包含小写字母，因此 ∣Σ∣≤26。我们需要 O(∣Σ∣) 的空间存储哈希映射。

使用哈希表存储索引

思路与算法

我们可以对方法一进行修改，使得第二次遍历的对象从字符串变为哈希映射。

具体地，对于哈希映射中的每一个键值对，键表示一个字符，值表示它的首次出现的索引（如果该字符只出现一次）或者 −1（如果该字符出现多次）。当我们第一次遍历字符串时，设当前遍历到的字符为 c，如果 c 不在哈希映射中，我们就将 c 与它的索引作为一个键值对加入哈希映射中，否则我们将 c 在哈希映射中对应的值修改为 −1。

在第一次遍历结束后，我们只需要再遍历一次哈希映射中的所有值，找出其中不为 −1 的最小值，即为第一个不重复字符的索引，然后返回该索引对应的字符。如果哈希映射中的所有值均为 −1，我们就返回空格。

class Solution {
public:
    char firstUniqChar(string s) {
        unordered_map<char, int> position;
        int n = s.size();
        for (int i = 0; i < n; ++i) {
            if (position.count(s[i])) {
                position[s[i]] = -1;
            }
            else {
                position[s[i]] = i;
            }
        }
        int first = n;
        for (auto [_, pos]: position) {
            if (pos != -1 && pos < first) {
                first = pos;
            }
        }
        return first == n ? ' ' : s[first];
    }
};

复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 s 的长度。第一次遍历字符串的时间复杂度为 O(n)，第二次遍历哈希映射的时间复杂度为 O(∣Σ∣)，由于 s 包含的字符种类数一定小于 s 的长度，因此 O(∣Σ∣) 在渐进意义下小于 O(n)，可以忽略。
  • 空间复杂度：O(∣Σ∣)，其中 Σ 是字符集，在本题中 ss 只包含小写字母，因此 ∣Σ∣≤26。我们需要 O(∣Σ∣) 的空间存储哈希映射。

队列

思路与算法

我们也可以借助队列找到第一个不重复的字符。队列具有「先进先出」的性质，因此很适合用来找出第一个满足某个条件的元素。

具体地，我们使用与方法二相同的哈希映射，并且使用一个额外的队列，按照顺序存储每一个字符以及它们第一次出现的位置。当我们对字符串进行遍历时，设当前遍历到的字符为 c，如果 c 不在哈希映射中，我们就将 c 与它的索引作为一个二元组放入队尾，否则我们就需要检查队列中的元素是否都满足「只出现一次」的要求，即我们不断地根据哈希映射中存储的值（是否为 −1）选择弹出队首的元素，直到队首元素「真的」只出现了一次或者队列为空。

在遍历完成后，如果队列为空，说明没有不重复的字符，返回空格，否则队首的元素即为第一个不重复的字符以及其索引的二元组。

class Solution {
public:
    char firstUniqChar(string s) {
        unordered_map<char, int> position;
        queue<pair<char, int>> q;
        int n = s.size();
        for (int i = 0; i < n; ++i) {
            if (!position.count(s[i])) {
                position[s[i]] = i;
                // 知识点1：emplace的使用
                q.emplace(s[i], i);
            }
            else {
                position[s[i]] = -1;
                while (!q.empty() && position[q.front().first] == -1) {
                    q.pop();
                }
            }
        }
        return q.empty() ? ' ' : q.front().first;
    }
};

复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 s 的长度。遍历字符串的时间复杂度为O(n)，而在遍历的过程中我们还维护了一个队列，由于每一个字符最多只会被放入和弹出队列最多各一次，因此维护队列的总时间复杂度为 O(∣Σ∣)，由于 s 包含的字符种类数一定小于 s 的长度，因此 O(∣Σ∣) 在渐进意义下小于 O(n)，可以忽略。
  • 空间复杂度：O(∣Σ∣)，其中 Σ 是字符集，在本题中 s 只包含小写字母，因此∣Σ∣≤26。我们需要 O(∣Σ∣) 的空间存储哈希映射以及队列。

知识点拓展

1. emplace的使用

image-20220317173713180

两者的区别

当调用insert时，是将对象传递给insert，对象被拷贝到容器中，而当我们使用emplace时，是将参数传递给构造函数，emplace使用这些参数在容器管理的内存空间中直接构造元素。

emplace_back能通过参数构造对象，不需要拷贝或者移动内存，相比push_back能更好地避免内存的拷贝与移动，使容器插入元素的性能得到进一步提升。使用emplace比常规的push_back少调用了一次复制构造函数。

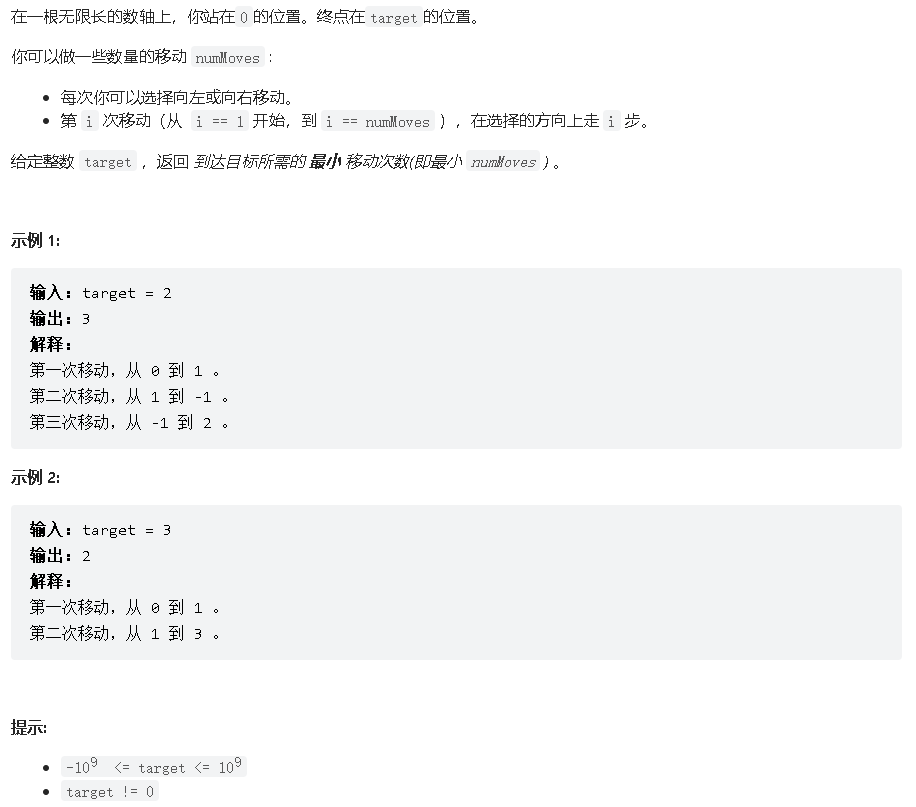
到达终点数字

LeetCode 754. reach-a-number

题目：

image-20220317174458626

题解

分析 + 数学

IMG_3454 
class Solution {
public:
    int reachNumber(int target) {
        int n = 0;
        int ar[46341] = {0};
        for(int i=0; i<46341; i++){
            ar[i] = (i*(i+1))/2;
        }       
        while(ar[n] < abs(target)){
            n++;
        }
        while((ar[n-1]+n)%2 != abs(target)%2){
            n++;
        } 
        return n;
    }
};

复杂度分析

image-20220318160212156

分析 + 数学（进一步优化）

image-20220318155953444

int reachNumber(int target){
    target = abs(target);
    int s, dt;
    // 1+2+...+n求和公式Sn = n*(n+1)/2
    // 由求和公式逆推得n = sqrt(2*Sn - 0.25) - 0.5
    s = sqrt(2 * target + 0.25) - 0.5;
    s += s * (s + 1)/2 < target? 1:0;
    dt = s * (s + 1)/2 - target;
    return dt % 2 == 0? s: s + 1 + s % 2;
}

复杂度分析

  • 时间复杂度：O(1)。
  • 空间复杂度：O(1)。

最长公共子序列

LeetCode 1143. longest-common-subsequence

题目：

image-20220318161832955

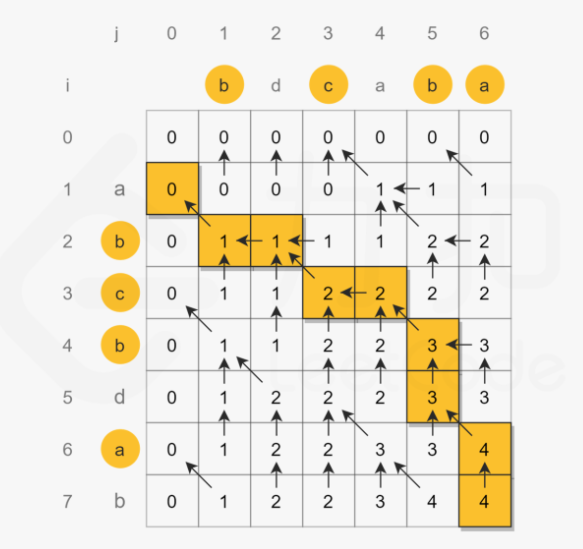
题解

动态规划

class Solution {
public:
    int pu(string t1, string t2){
        int n1 = t1.size();
        int n2 = t2.size();
        int dp[n1][n2];
        dp[0][0] = (t1[0] == t2[0] ? 1 : 0);
        for(int i = 1; i < n1; i++){
            dp[i][0] = max(dp[i-1][0], t1[i] == t2[0] ? 1 : 0);
        }
        for(int j = 1; j < n2; j++){
            dp[0][j] = max(dp[0][j-1], t1[0] == t2[j] ? 1 : 0);
        }
        for(int i = 1; i < n1; i++){
            for(int j = 1; j < n2; j++){
                dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
                if(t1[i] == t2[j])
                    dp[i][j] = max(dp[i-1][j-1] + 1, dp[i][j]);
            }
        }
        return dp[n1-1][n2-1];
    }

    int longestCommonSubsequence(string text1, string text2) {
        return pu(text1, text2);
    }
};

官方代码：

image-20220318163315889 
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.length(), n = text2.length();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            char c1 = text1.at(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.at(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
};

复杂度分析

  • 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 text 1和 text 2的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
  • 空间复杂度：O(mn)，其中 m 和 n 分别是字符串 text 1和 text 2的长度。创建了 m+1 行 n+1 列的二维数组 dp。

编辑距离

LeetCode 72. edit-distance

题目：

image-20220318164215871

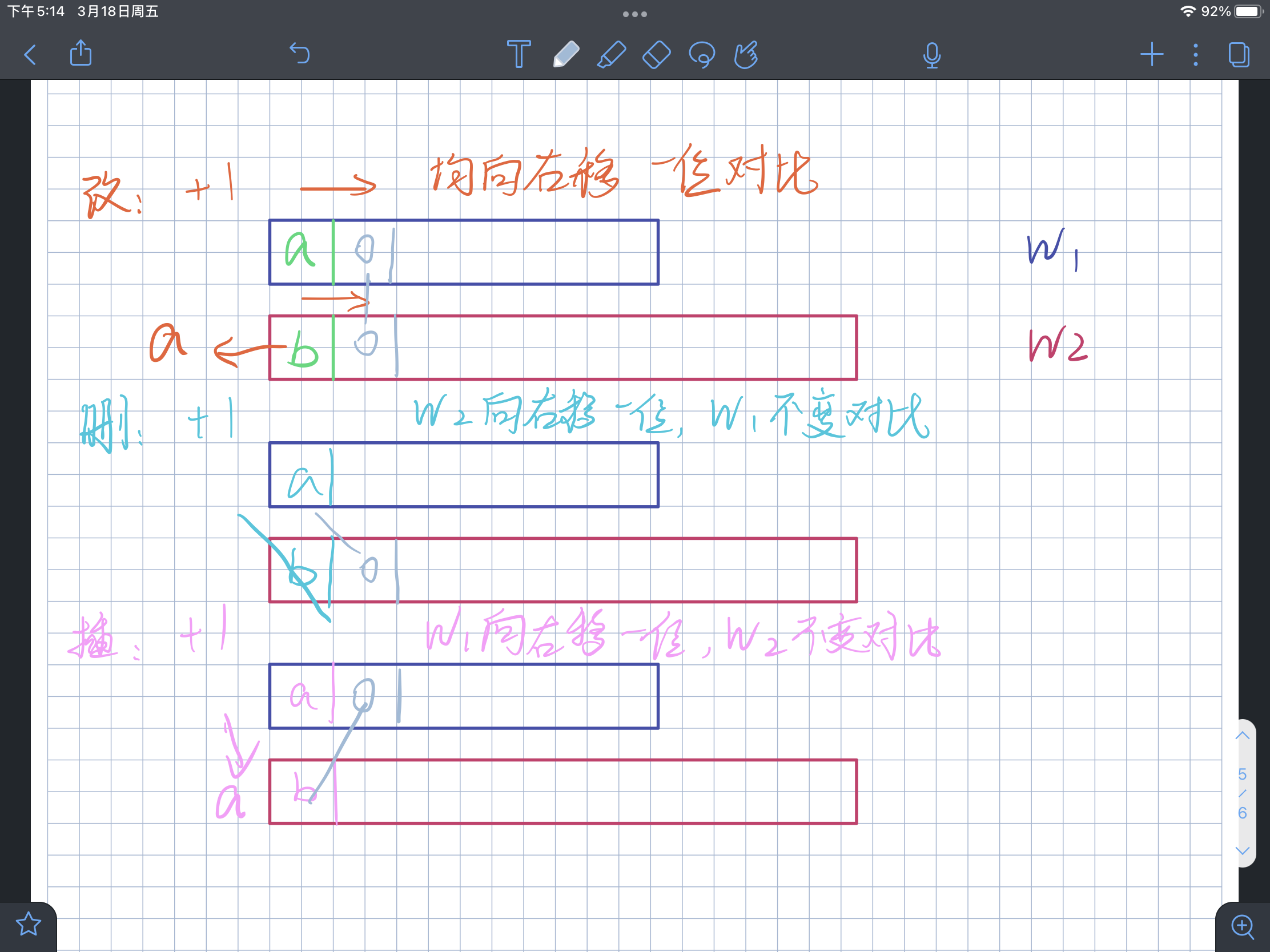
题解

递归到动态规划的过程参考：从暴力递归到动态规划

IMG_3455

暴力递归

class Solution {
public:
    int le(string w, string target){
        int n1 = w.size();
        int n2 = target.size();
        int temp = 0;
        if(n1 == 0)
            return  n2 - n1;
        if(n2 == 0)
            return  n1 - n2;
        string w1 = w.substr(1,n1-1);
        string t1 = target.substr(1,n2-1);
        if(w[0] == target[0])
            return le(w1, t1);
        if(w[0] != target[0])
            // 改、 删、 插 
            return min(min(le(w1, t1) + 1, le(w1, target) + 1), le(w, t1) + 1);
        return 0;
    }
    int minDistance(string word1, string word2) {
        return le(word1, word2);
    }
};

带记忆数组的递归

存储已经算过的值，再次调用时直接返回值

class Solution {
public:
    unordered_map<string, int> map;
    int le(string w, string target){

        int n1 = w.size();
        int n2 = target.size();
        int temp = 0;
        auto it =map.find(w+"_"+target);
         if(it != map.end())
             return it->second;
        if(n1 == 0)
            map[w+"_"+target] = n2 - n1;
            return map[w+"_"+target];
        if(n2 == 0)
            map[w+"_"+target] = n1 - n2;
            return map[w+"_"+target];
        string w1 = w.substr(1,n1-1);
        string t1 = target.substr(1,n2-1);
        if(w[0] == target[0])
            temp = le(w1, t1);
            map[w+"_"+target] = temp;
            return map[w+"_"+target];
        if(w[0] != target[0])
            // 改、 删、 插
            temp = min(min(le(w1, t1) + 1, le(w1, target) + 1), le(w, t1) + 1);
            map[w+"_"+target] = temp;
            return map[w+"_"+target];
        return 0;
    }
    int minDistance(string word1, string word2) {
        return le(word1, word2);
    }
}；

动态规划

官方解答：

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.length();
        int m = word2.length();

        // 有一个字符串为空串
        if (n * m == 0) return n + m;

        // DP 数组
        vector<vector<int>> D(n + 1, vector<int>(m + 1));

        // 边界状态初始化
        for (int i = 0; i < n + 1; i++) {
            D[i][0] = i;
        }
        for (int j = 0; j < m + 1; j++) {
            D[0][j] = j;
        }

        // 计算所有 DP 值
        for (int i = 1; i < n + 1; i++) {
            for (int j = 1; j < m + 1; j++) {
                int left = D[i - 1][j] + 1;
                int down = D[i][j - 1] + 1;
                int left_down = D[i - 1][j - 1];
                if (word1[i - 1] != word2[j - 1]) left_down += 1;
                D[i][j] = min(left, min(down, left_down));

            }
        }
        return D[n][m];
    }
};

复杂度分析

  • 时间复杂度 ：O(mn)，其中 m 为 word1 的长度，n 为 word2 的长度。
  • 空间复杂度 ：O(mn)，我们需要大小为 O(mn) 的 D 数组来记录状态值。