算法DAY-07

算法总结 DAY_07

链表专题

一、反转链表

LeetCode 206. reverse-linked-list

题目：

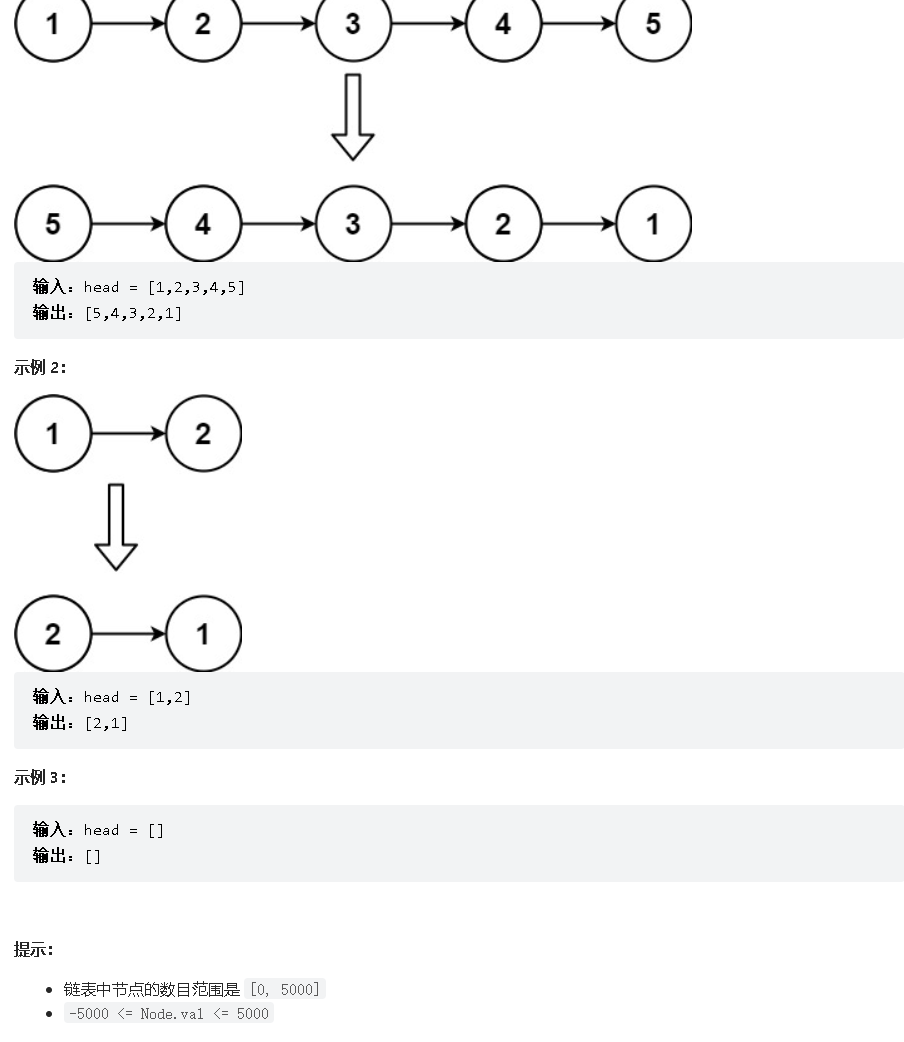
题解

1. 迭代

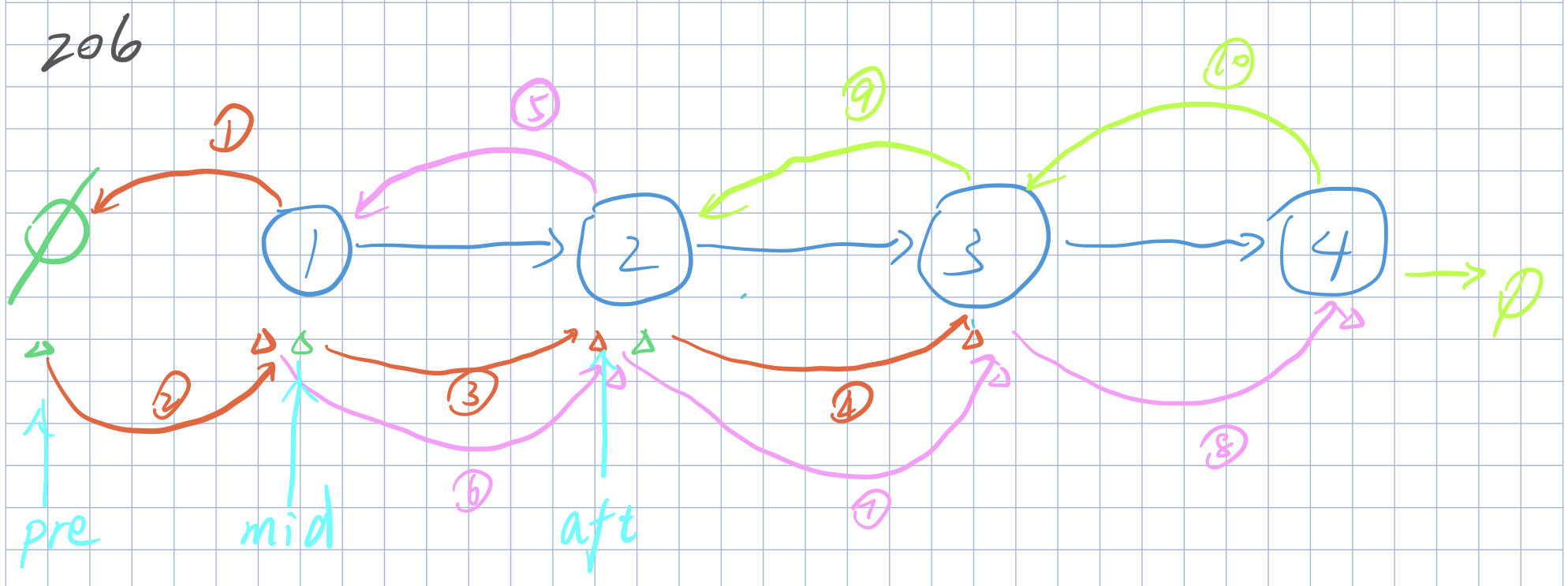
在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head)
            return head;
        ListNode* mid = head;       // 需翻转的节点
        ListNode* pre = nullptr;    // 前一个节点  
        ListNode* aft = head->next; // 后一个节点
        while(aft){
            mid->next = pre;
            pre = mid;
            mid = aft;
            aft = aft->next;
        }
        mid->next = pre;
        return mid;
    }
};

复杂度分析

• 时间复杂度：O(n)，其中 n 是链表的长度。需要遍历链表一次。
• 空间复杂度：O(1)。

2.递归

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return newHead;
    }
};

复杂度分析

• 时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。
• 空间复杂度：O(n)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

二、反转链表 II

LeetCode 92. reverse-linked-list-ii

题目：

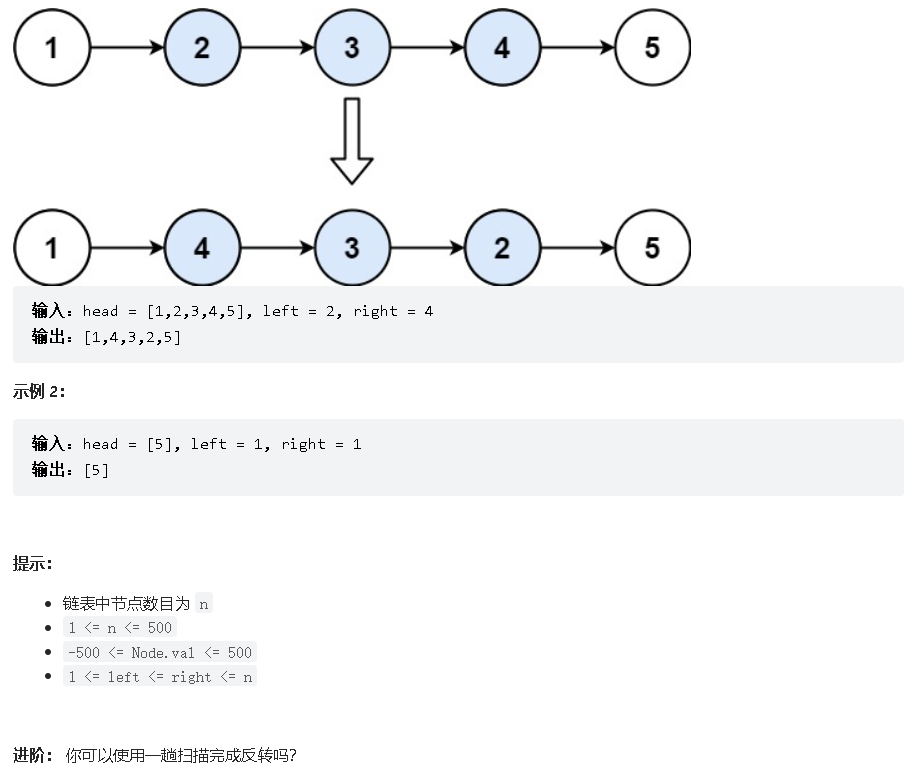
题解

使用「206. 反转链表」的解法，反转 left 到 right 部分以后，再拼接起来。我们还需要记录 left 的前一个节点，和 right 的后一个节点。如图所示：

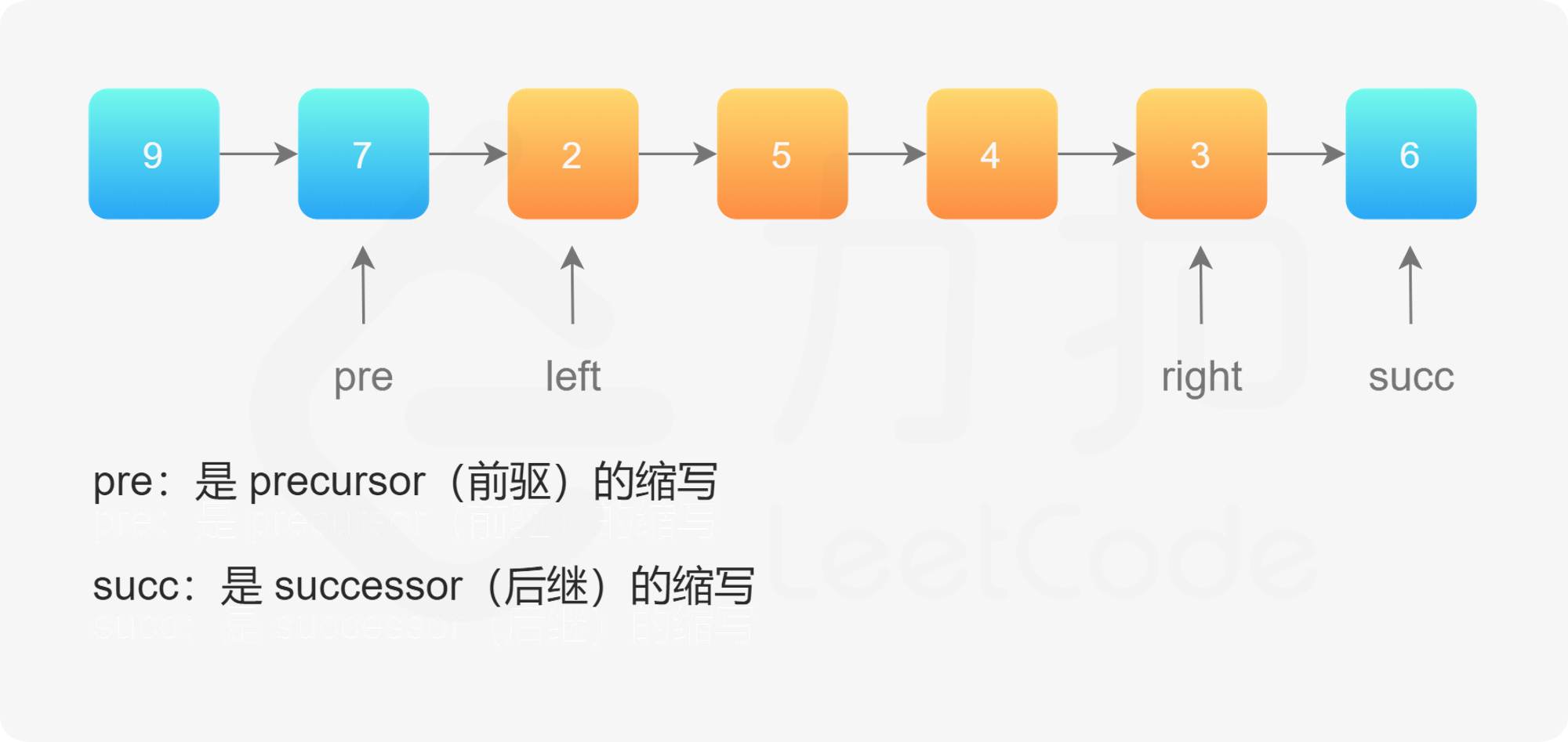
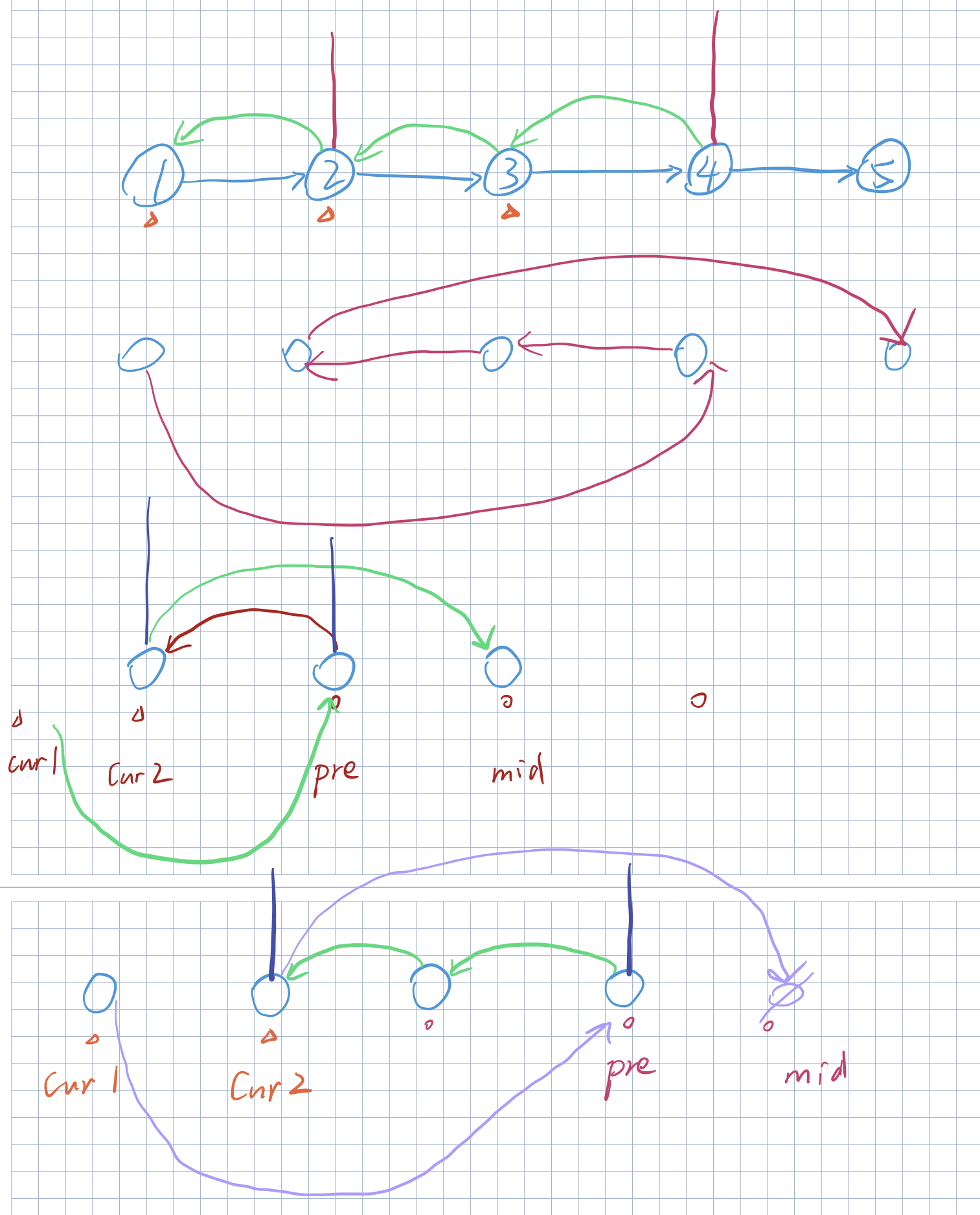
1. 迭代

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        //ListNode* ans = head;
        int Count = 0;
        if(!head || left == right)
            return head;
        ListNode *pre = new ListNode(-1);              // 前一个节点  
        pre->next = head;
        //ListNode* aft = head->next; // 后一个节点
        for(int i=1; i<left; i++){
            pre = pre->next;
        }
        ListNode* cur1 = pre;
        ListNode* cur2 = pre->next;
        pre = pre->next;
        ListNode* mid = pre->next;
        ListNode* aft = pre->next->next;
        for(int i=1; i<right-left; i++){
            mid->next = pre;
            pre = mid;
            mid = aft;
            aft = aft->next;
        }
        mid->next = pre;
        pre = mid;
        mid = aft;
        cur2->next = mid;
        cur1->next = pre;
        if(cur1->val == -1){
            return cur1->next;
        }else
            return head;
    }
};

官方题解：

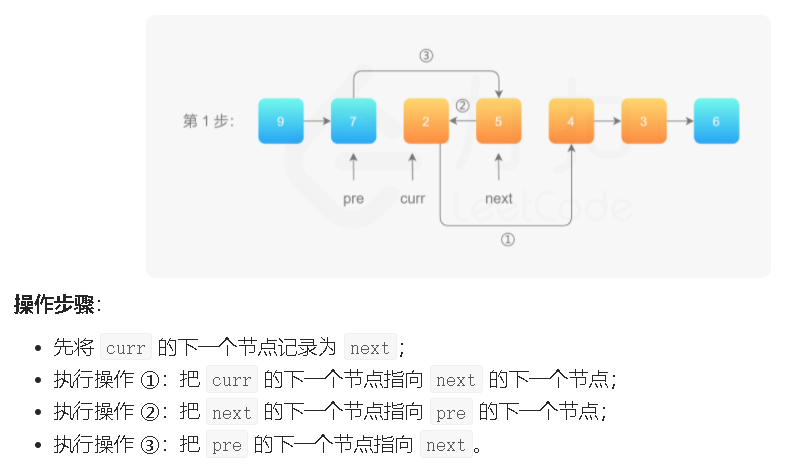
class Solution {
public:
    ListNode *reverseBetween(ListNode *head, int left, int right) {
        // 设置 dummyNode 是这一类问题的一般做法
        ListNode *dummyNode = new ListNode(-1);
        dummyNode->next = head;
        ListNode *pre = dummyNode;
        for (int i = 0; i < left - 1; i++) {
            pre = pre->next;
        }
        ListNode *cur = pre->next;
        ListNode *next;
        for (int i = 0; i < right - left; i++) {
            next = cur->next;
            cur->next = next->next;
            next->next = pre->next;
            pre->next = next;
        }
        return dummyNode->next;
    }
};

复杂度分析：

• 时间复杂度：O(N)，其中 N 是链表总节点数。最多只遍历了链表一次，就完成了反转。
• 空间复杂度：O(1)。只使用到常数个变量。

三、相交链表

LeetCode 160. intersection-of-two-linked-lists

题目：

题解

1. 哈希表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        map<ListNode*, int> map;
        while(headA){
            map[headA] ++;
            headA = headA->next;
        }  
        while(headB){
            map[headB] ++;
            if(map[headB] > 1)
                return headB;
            headB = headB->next;
        }
        return NULL;
    }
};

复杂度分析

• 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。需要遍历两个链表各一次。
• 空间复杂度：O(m)，其中 m 是链表 headA 的长度。需要使用哈希集合存储链表 headA 中的全部节点。

2. 双指针

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *pA = headA, *pB = headB;
        while (pA != pB) {
            pA = pA == nullptr ? headB : pA->next;
            pB = pB == nullptr ? headA : pB->next;
        }
        return pA;
    }
};

复杂度分析

• 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。
• 空间复杂度：O(1)。

四、环形链表 II

LeetCode 142. linked-list-cycle-ii

题目：

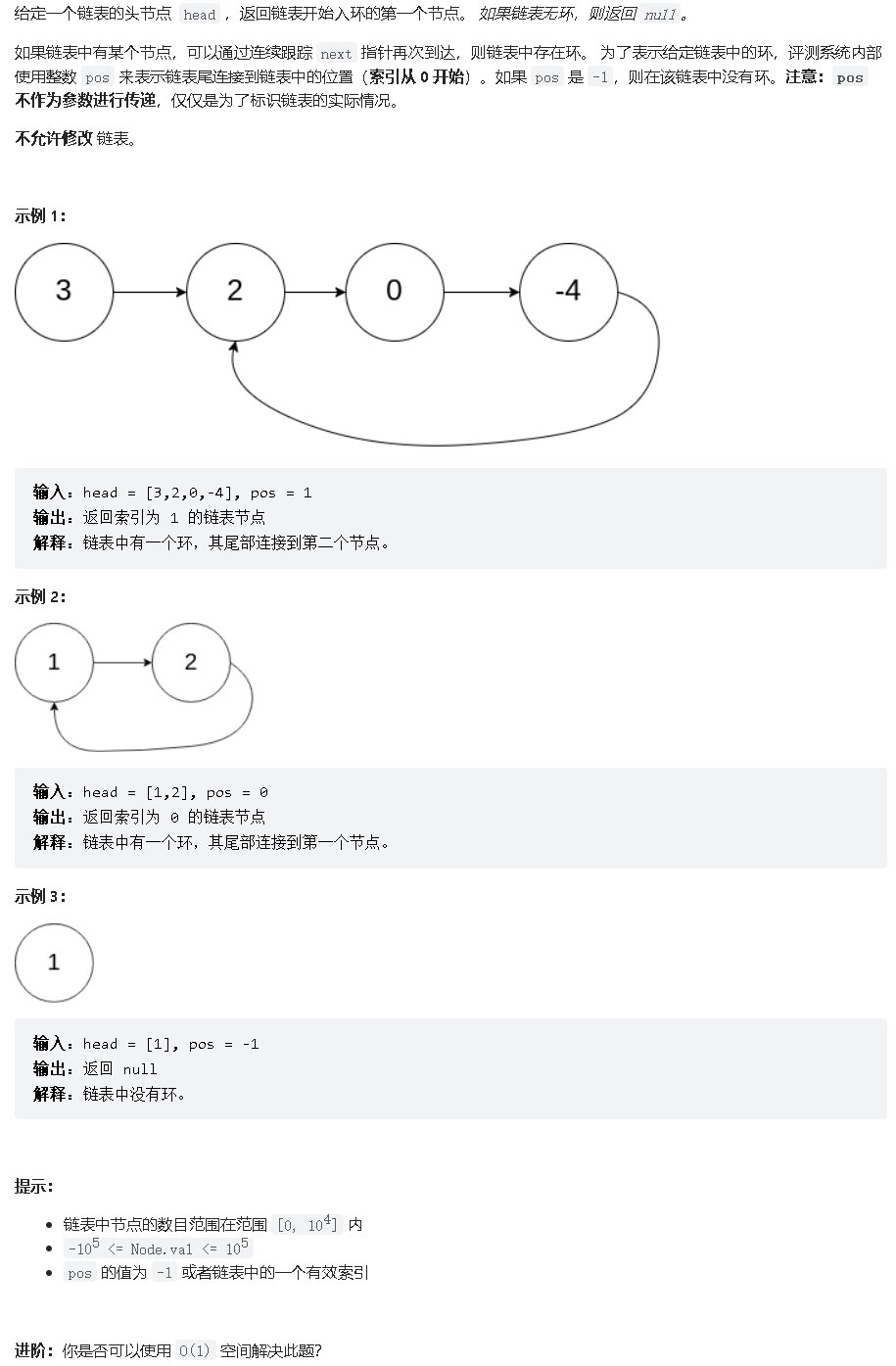
题解

1. 哈希表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_map<ListNode*, int> map;
        while(head){
            map[head]++;
            if(map[head] > 1)
                return head;
            head = head->next;
        }
        return NULL;
    }
};

复杂度分析

• 时间复杂度：O(N)，其中 N 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。
• 空间复杂度：O(N)，其中 N 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。

2. 快慢指针

原理解释参照：https://chenduowen233.github.io/DAY-03/

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head || !head->next)
            return NULL;
        else{
            ListNode* cur1 = head;
            ListNode* cur2 = head;
            while(cur2){
                cur1 = cur1->next;
                if(cur2->next == NULL)
                    return NULL;
                cur2 = cur2->next->next;
                if(cur1 == cur2){
                    ListNode* cur3 = head;
                    while(cur2 != cur3){
                        cur2 = cur2->next;
                        cur3 = cur3->next;
                    }
                    return cur3;
                }
            }
        }
        return NULL;
    }
};

五、排序链表

LeetCode 148. sort-list

题目：

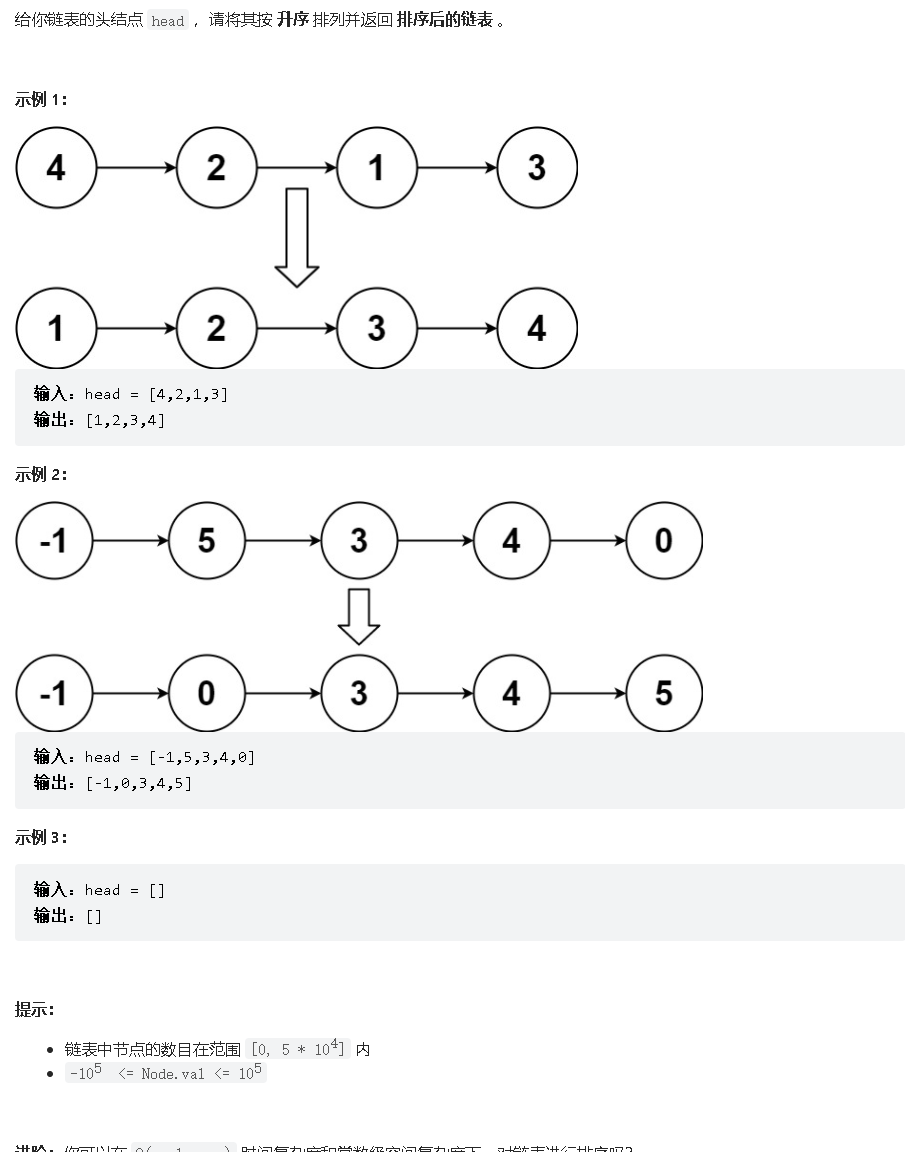
题解

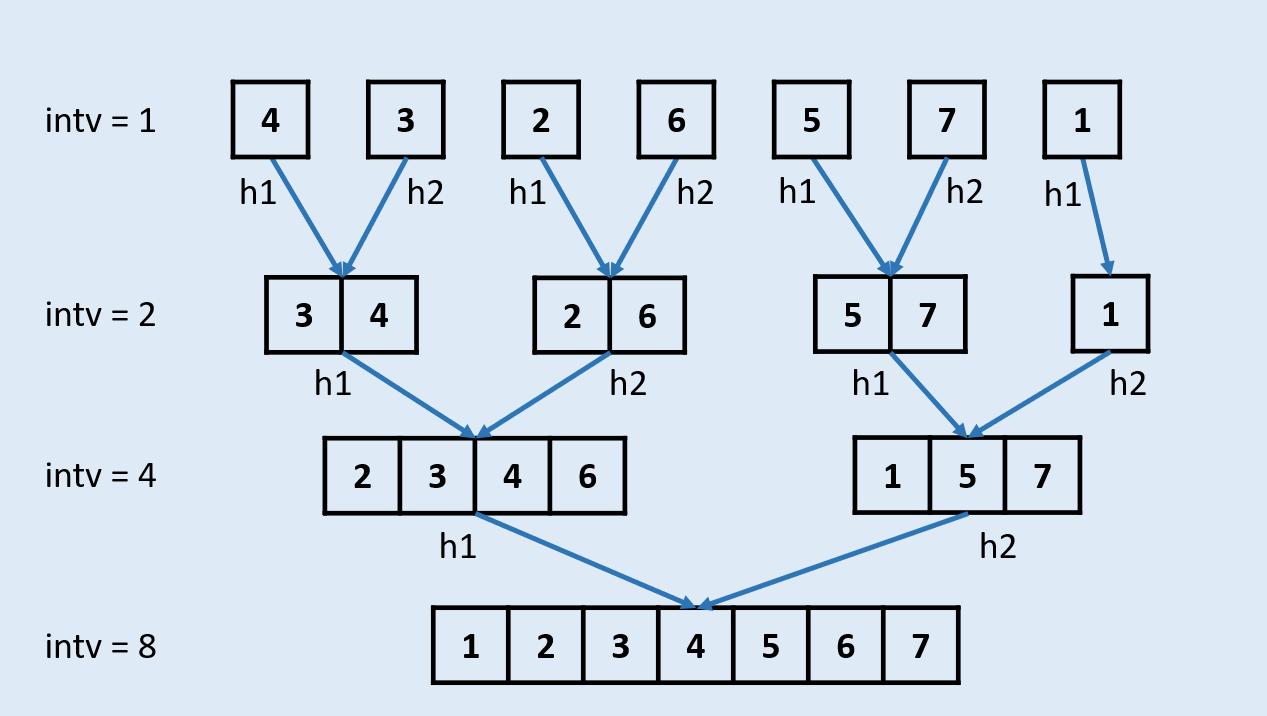
1. 自底向上归并排序

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        if (head == nullptr) {
            return head;
        }
        int length = 0;
        ListNode* node = head;
        while (node != nullptr) {
            length++;
            node = node->next;
        }
        ListNode* dummyHead = new ListNode(0, head);
        for (int subLength = 1; subLength < length; subLength <<= 1) {
            ListNode* prev = dummyHead, *curr = dummyHead->next;
            while (curr != nullptr) {
                ListNode* head1 = curr;
                for (int i = 1; i < subLength && curr->next != nullptr; i++) {
                    curr = curr->next;
                }
                ListNode* head2 = curr->next;
                curr->next = nullptr;
                curr = head2;
                for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
                    curr = curr->next;
                }
                ListNode* next = nullptr;
                if (curr != nullptr) {
                    next = curr->next;
                    curr->next = nullptr;
                }
                ListNode* merged = merge(head1, head2);
                prev->next = merged;
                while (prev->next != nullptr) {
                    prev = prev->next;
                }
                curr = next;
            }
        }
        return dummyHead->next;
    }

    ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }
};

复杂度分析

• 时间复杂度：O(n log n)，其中 n 是链表的长度。
• 空间复杂度：O(1)。

2. 自顶向下归并排序

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        return sortList(head, nullptr);
    }

    ListNode* sortList(ListNode* head, ListNode* tail) {
        if (head == nullptr) {
            return head;
        }
        if (head->next == tail) {
            head->next = nullptr;
            return head;
        }
        ListNode* slow = head, *fast = head;
        while (fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next;
            }
        }
        ListNode* mid = slow;
        return merge(sortList(head, mid), sortList(mid, tail));
    }

    ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }
};

复杂度分析

• 时间复杂度：O(nlogn)，其中 n 是链表的长度。
• 空间复杂度：O(logn)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。

知识点拓展

1. 归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，归并排序对序列的元素进行逐层折半分组，然后从最小分组开始比较排序，合并成一个大的分组，逐层进行，最终所有的元素都是有序的

算法原理

然后从下往上逐层合并，首先对第一层序列1（只包含元素4）和序列2（只包含元素5）进行合并

创建一个大序列，序列长度为两个小序列长度之和，p1、p2指针分别指向两个小序列的第一个元素，p指向大序列的第一个元素

比较p1、p2指向的元素，4小于5，将4填入p指向的元素，p、p1往右移一位

此时，序列1已经没有元素，将序列2的元素依次填入大序列中

序列8和1，序列7和2，序列6和3，用同样的方式填入新的序列

接着，以4、5为序列1，1、8为序列2，继续进行合并

创建一个序列长度为4的大序列，p1指向序列1的第一个元素4，p2指向序列2的第一个元素1，p指向大序列的第一个元素

4和1比较，4大于1，1填入p指向的元素，p、p2往右移一位

4和8比较，4小于8，4填入p指向的元素，p、p1往右移一位

5和8比较，5小于8，5填入p指向的元素，p、p1往右移一位

自此，序列1已经没有元素，将序列2的元素依次填入大序列中

序列2、7和序列3、6以同样的方式合并成新的序列

最后，将序列1、4、5、8和序列2、3、6、7以同样的方式继续合并成新的序列

至此所有的元素都是有序的

function sort(arr, startIndex = 0, endIndex = arr.length - 1) {
    // 递归结束条件：startIndex大于等于endIndex的时候
    if (startIndex >= endIndex) {
        return;
    }

    // 折半递归
    let midIndex = parseInt((startIndex + endIndex) / 2);
    sort(arr, startIndex, midIndex);
    sort(arr, midIndex + 1, endIndex);
    // 将两个有序的小数组，合并成一个大数组
    merge(arr, startIndex, midIndex, endIndex);
}

function merge(arr, startIndex, midIndex, endIndex) {
    // 新建一个大数组
    let tempArr = [];
    let p1 = startIndex;
    let p2 = midIndex + 1;
    let p = 0;

    // 比较两个有序小数组的元素，依次放入大数组中
    while (p1 <= midIndex && p2 <= endIndex) {
        if (arr[p1] <= arr[p2]) {
            tempArr[p++] = arr[p1++];
        } else {
            tempArr[p++] = arr[p2++];
        }
    }

    // 右侧小数组已排序完毕，左侧小数组还有剩余，将左侧小数组元素依次放入大数组尾部
    while (p1 <= midIndex) {
        tempArr[p++] = arr[p1++];
    }
    // 左侧小数组已排序完毕，右侧小数组还有剩余，将右侧小数组元素依次放入大数组尾部
    while (p2 <= endIndex) {
        tempArr[p++] = arr[p2++];
    }

    for (let i = 0; i < tempArr.length; i++) {
        arr[i + startIndex] = tempArr[i];
    }
}

let arr = [4, 5, 8, 1, 7, 2, 6, 3];
sort(arr);
console.log(arr);

参考链接：(50条消息) 十大经典排序算法-归并排序算法详解_小小学编程的博客-CSDN博客_归并排序算法

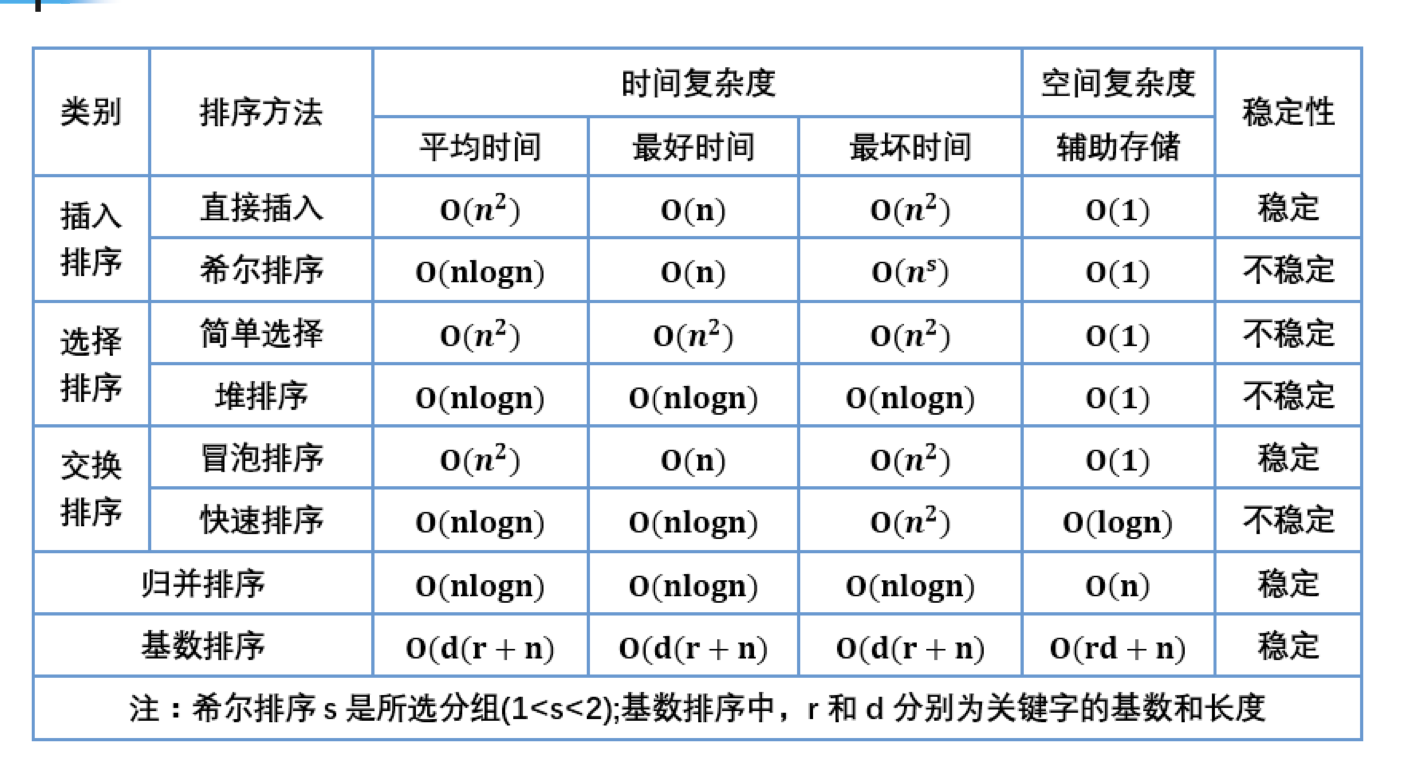
常见排序算法时间、空间复杂度：