算法总结 DAY_04

二分专题

复杂度log(n)：二分法的”代言词“

二分模板：

int l = 0;
      int r = nums.size() - 1;
      int mid;
      while(l <= r){
          mid = l + (r - l) / 2;  //左中点
          if(target == nums[mid])
              return mid;
          if(target < nums[mid])
              r = mid - 1;
          if(target > nums[mid])
              l = mid + 1;    
      }
      return l;

详细讲解文章链接：

关于二分法三个模板更详细的说明

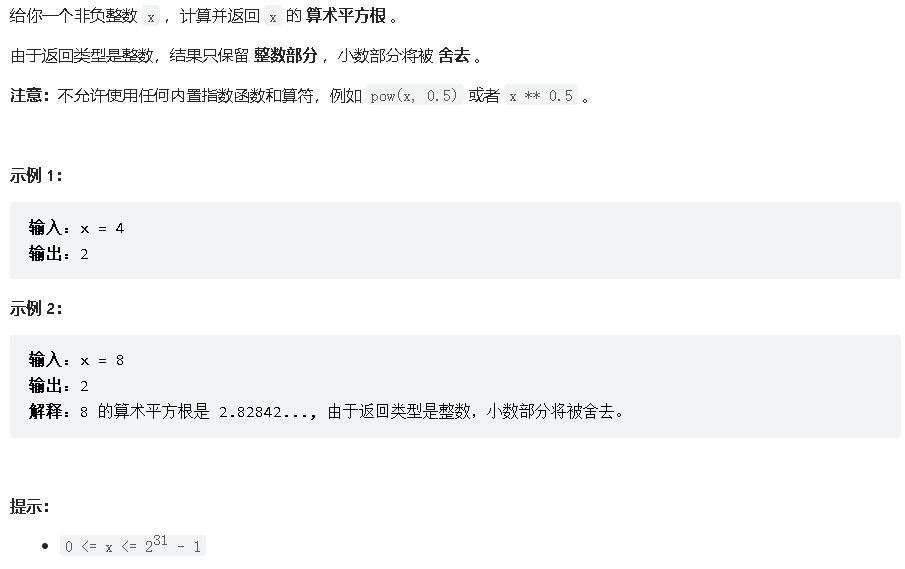
x 的平方根

LeetCode 69. sqrtx

题目：

题解

二分法

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long long)mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
};

复杂度分析

时间复杂度：O(logx)，即为二分查找需要的次数。
空间复杂度：O(1)。

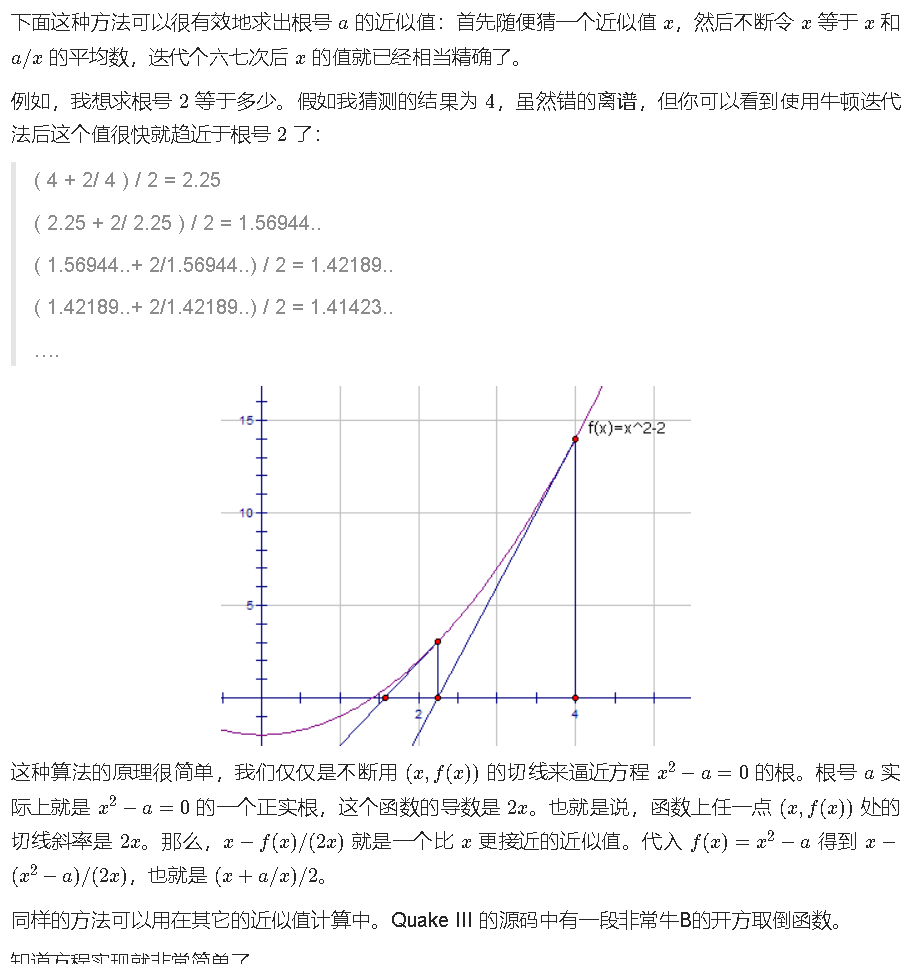
牛顿迭代

class Solution {
public:
    int mySqrt(int a) {
        long x = a;
        while (x * x > a) x = (x + a / x) / 2;
        return (int)x;
    }
};

复杂度分析

时间复杂度：O(log x)，此方法是二次收敛的，相较于二分查找更快。
空间复杂度：O(1)。

雷神之锤3 算法

float InvSqrt(float x)
{
float xhalf = 0.5f*x;
int i = *(int*)&x; // get bits for floating VALUE
i = 0x5f375a86- (i>>1); // gives initial guess y0
x = *(float*)&i; // convert bits BACK to float
x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
return x;
}

参考资料：平方根倒数速算法

快速平方根倒数算法 - 知乎 (zhihu.com)

搜索插入位置

LeetCode 35. search-insert-position

题目：

题解

二分法

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l = 0;
        int r = nums.size() - 1;
        int mid;
        while(l <= r){
            mid = l + (r - l) / 2;
            if(target == nums[mid])
                return mid;
            if(target < nums[mid])
                r = mid - 1;
            if(target > nums[mid])
                l = mid + 1;    
        }
        return l;
    }
};

复杂度分析

时间复杂度：O(logn)，其中 n 为数组的长度。二分查找所需的时间复杂度为 O(logn)。
空间复杂度：O(1)。我们只需要常数空间存放若干变量。

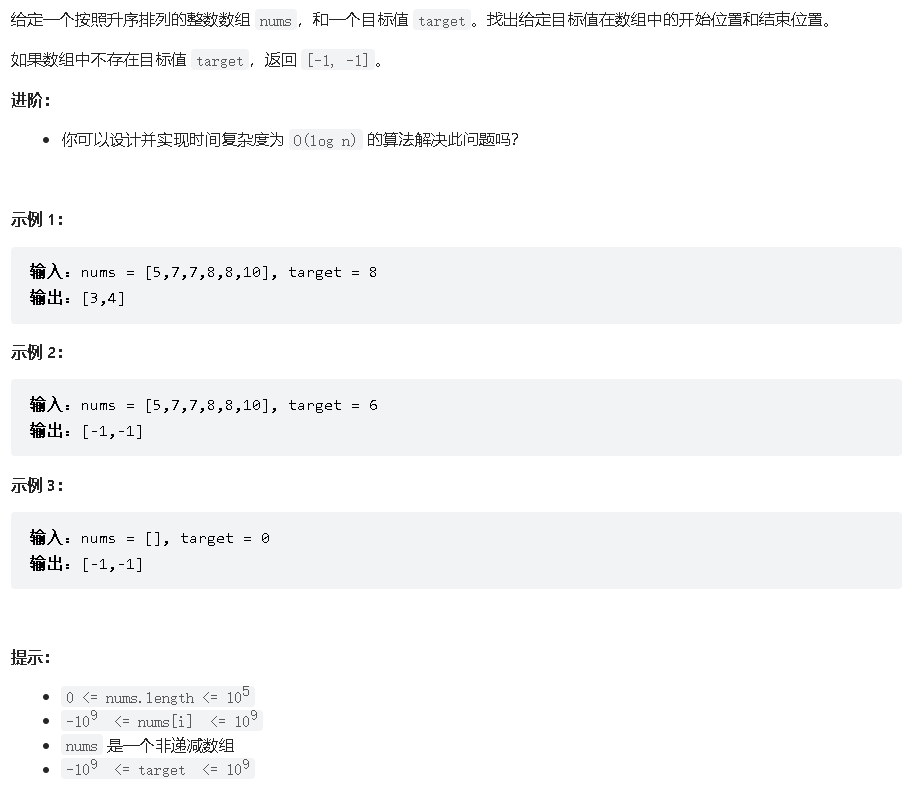
在排序数组中查找元素的第一个和最后一个位置

LeetCode 34. find-first-and-last-position-of-element-in-sorted-array

题目：

题解

二分法

因为数组都是整数，可以用{target-0.5, target+0.5}两个值来确定位置；

也可以先找到第一个与target的值，再慢慢向两边扩直到不等于target；

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int mid;
        int ans[2] = {-1};
        double t[2] = {target-0.5, target+0.5};
        for(int i = 0; i < 2; i++){
            int l = 0;
            int r = nums.size()-1;
            while(l <= r){
                mid = l + (r - l) / 2;
                if(t[i] < nums[mid])
                    r = mid - 1;
                if(t[i] > nums[mid])
                    l = mid + 1;    
            }
            ans[i] = l - i;
        }
        if(ans[0] > ans[1])
            return {-1, -1};
        return {ans[0],ans[1]};
    }
};

复杂度分析

时间复杂度： O(logn) ，其中 n 为数组的长度。二分查找的时间复杂度为O(logn)，一共会执行两次，因此总时间复杂度为 O(logn)。
空间复杂度：O(1) 。只需要常数空间存放若干变量。

搜索二维矩阵

LeetCode 74. search-a-2d-matrix

题目：

题解

两次二分查找

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        int n = matrix[0].size();
        int h = 0;
        int l = 0;
        int r = m - 1;
        int mid;
        if(m != 1){
            while(l <= r){
                mid = l + (r - l) / 2;
                if(target == matrix[mid][n-1])
                    return true;
                if(target < matrix[mid][n-1])
                    r = mid - 1;
                if(target > matrix[mid][n-1])
                    l = mid + 1;    
            }
        }
        h = l;
        if(h >= m)
            return false;
        l = 0;
        r = n - 1;
        if(n != 1){
            while(l <= r){
                mid = l + (r - l) / 2;
                if(target == matrix[h][mid])
                    return true;
                if(target < matrix[h][mid])
                    r = mid - 1;
                if(target > matrix[h][mid])
                    l = mid + 1;    
            }
        }
        if(target == matrix[h][0])
            return true;
        return false;
    }
};

官方题解：

class Solution {
public:
    bool searchMatrix(vector<vector<int>> matrix, int target) {
        auto row = upper_bound(matrix.begin(), matrix.end(), target, [](const int b, const vector<int> &a) {
            return b < a[0];
        });
        if (row == matrix.begin()) {
            return false;
        }
        --row;
        return binary_search(row->begin(), row->end(), target);
    }
};

复杂度分析

时间复杂度：O(logm+logn)=O(logmn)，其中 m 和 n 分别是矩阵的行数和列数。
空间复杂度：O(1)。

一次二分查找

思路

若将矩阵每一行拼接在上一行的末尾，则会得到一个升序数组，我们可以在该数组上二分找到目标元素。

代码实现时，可以二分升序数组的下标，将其映射到原矩阵的行和列上。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int low = 0, high = m * n - 1;
        while (low <= high) {
            int mid = (high - low) / 2 + low;
            int x = matrix[mid / n][mid % n];
            if (x < target) {
                low = mid + 1;
            } else if (x > target) {
                high = mid - 1;
            } else {
                return true;
            }
        }
        return false;
    }
};

复杂度分析

时间复杂度：O(log mn)，其中 m 和 n 分别是矩阵的行数和列数。
空间复杂度：O(1)。

搜索旋转排序数组

LeetCode 33. search-in-rotated-sorted-array

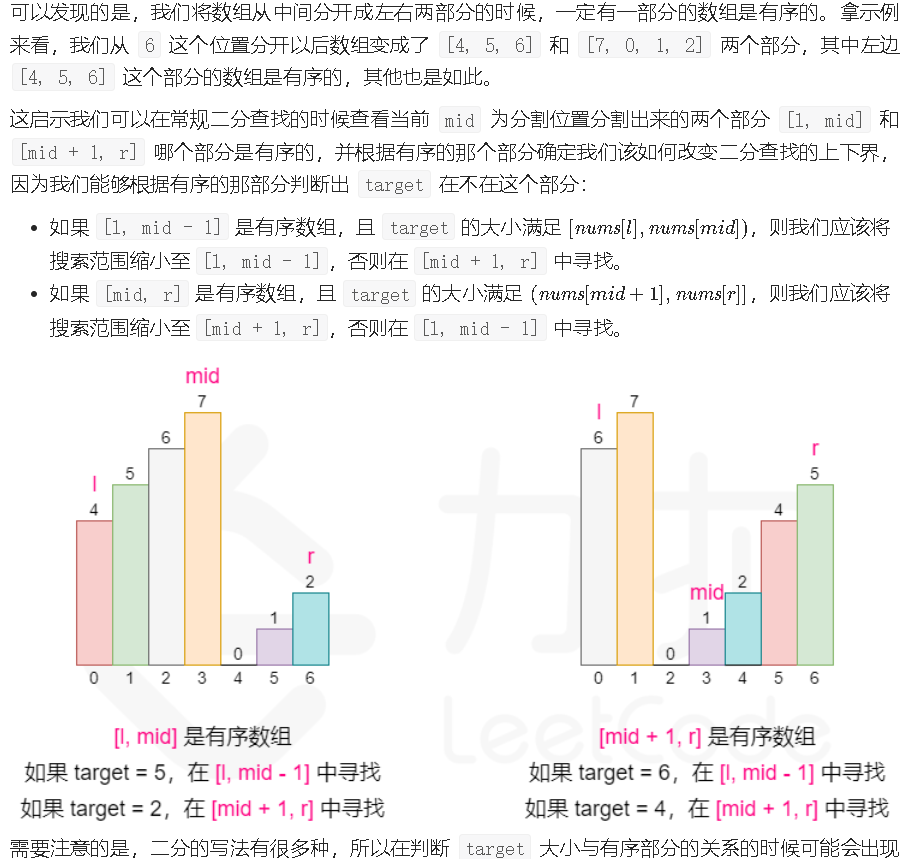
题目：

题解

二分法

思路和算法

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int l = 0;
        int r = nums.size() - 1;
        int mid;
        if(r == 0){
            return nums[0] == target ? 0 : -1;
        }
        while(l <= r){
            mid = l + (r - l) / 2;
            if(target == nums[mid])
                return mid;
            if(nums[0] <= nums[mid]){
                if(target >= nums[0] && target < nums[mid])
                    r = mid - 1;
                else
                    l = mid + 1;
            }
            else{
                if(target <= nums[nums.size()-1] && target > nums[mid])
                    l = mid + 1;
                else
                    r = mid - 1;    
            }
        }
        return -1;
    }
};