从暴力递归到动态规划
从暴力递归到动态规划
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决,是暴力递归的优化版本。所以做算题遇到不能直接写出的动态规划时,从暴力递归入手是个正确的选择,接下来我们看看两者的特点。
暴力递归
- 把问题转化为规模缩小了的同类问题的子问题
- 有明确的不需要继续进行递归的条件(base case)
- 有当得到了子问题的结果之后的决策过程
- 不记录每一个子问题的解
动态规化
- 从暴力递归中来
- 将每一个子问题的解记录下来,避免重复计算
- 把暴力递归的过程,抽象成了状态表达
- 并且存在化简状态表达,使其更加简洁的可能
解答流程
参考左神视频教程《程序员代码面试指南》作者:左神-左程云带你学习进大厂必问难点暴力递归到动态规划——IT名企算法与数据结构题目最优解_哔哩哔哩_bilibili
接着我们明确一般的解答流程:暴力递归解法->带记忆数组的递归解法->动态规划解法,只要按照这个流程去做基本都能解答出来。下面我以大家最为熟悉的斐波那契数列入手。 斐波那契数列的递推式是f(n)=f(n-1)+f(n-2)。(1,1,2,3,5,8…)
第一步:写出暴力递归解法
public int fibonacci(int n){ |
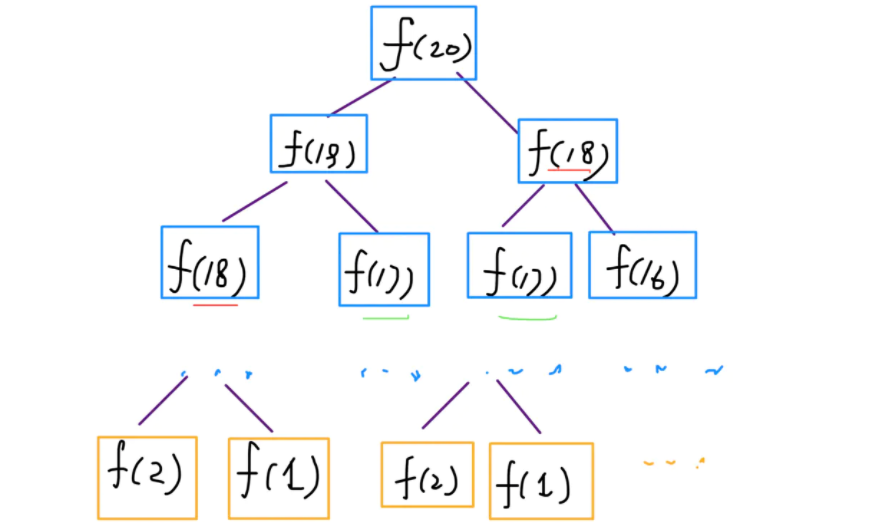
这个解法相信大部分人都能写出来,暴力递归之所以低效是因为存在大量的重复计算,借鉴LeetCode题解区一位大佬的图,如图所示,f(20)=f(19)+f(18),而f(19)=f(18)+f(17),这里就产生了重复计算,而且这种重复计算还很多,正是因为这些大量的重复计算,所以暴力递归很低效,这个算法的时间复杂度为 O(2^n)。
步骤二:带记忆数组的递归
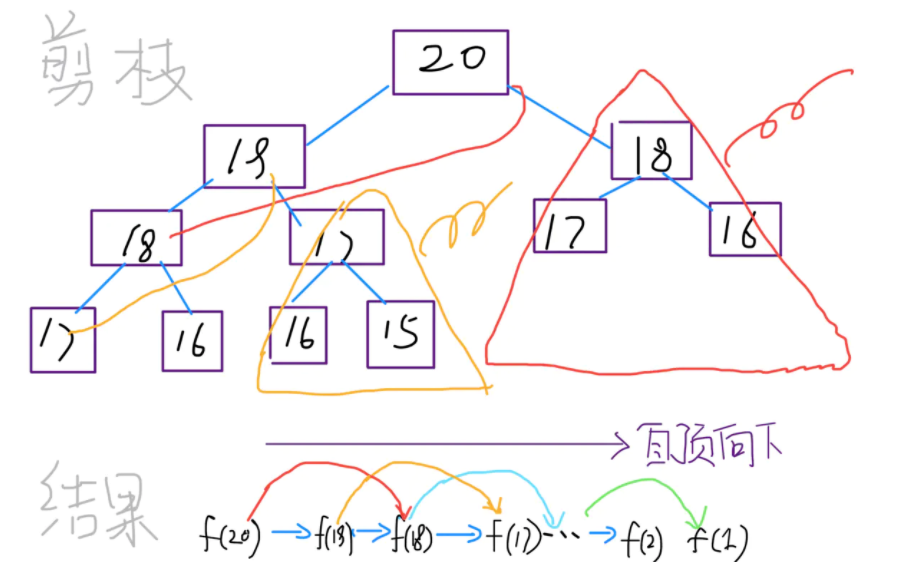
步骤一的计算过程中国充斥着大量的重复计算,解决重复计算的方法很简单,用一个数组或者其他容器装起来,递归的时候判断是否已经计算过的,如果已经计算过,就直接返回。这个是典型的用过空间换时间的做法,反应到上述递归图中就是“剪枝”了。(下图同样是借鉴的)
public int fibonacci(int n){ |
步骤三:转为动态规划
写出来了带记忆数组的递归解法,动态规划也就基本成型了,因为这两者区别不是很大,前者是自顶向下的,后者是自底向上的。自顶向下的意思是,比如求f(5),递归的做法是先递归到f(1),然后再往上走得到f(5);而动态规划是直接从f(1)开始往上求的。
public int fibonacci(int n){ |
参考链接:暴力递归如何转动态规划 - 云+社区 - 腾讯云 (tencent.com)
总结
动态规划一定能由递归转变,递归不一定能转变为动态规划。
带记忆数组的递归和动态规划相似,他两的时间复杂度也相差无几,动态规划中很关键的转移方程就是从暴力递归中而来的,所以当遇到没做过或者不能一下子写出转移方程的,从暴力递归做起总是一个正确的选择。






.JPG)

.JPG)




